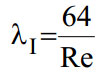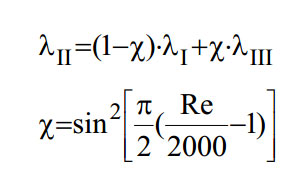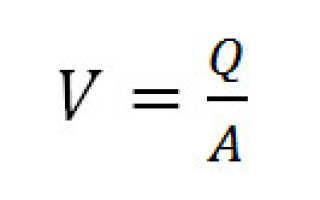Потери давления в трубопроводах
Онлайн расчет потерь напора по длине
Формулы для расчета потерь давления по длине
Данная автоматизированная система позволяет произвести расчет потерь напора по длине online. Расчет производится для трубопровода, круглого сечения, одинакового по всей длине диаметра, с постоянным расходом по всей длине (утечки или подпитки отсутствуют). Расчет производится для указанных жидкостей при температуре 20 град. С. Если вы хотите рассчитать потери напора при другой температуре, или для жидкости отсутствующей в списке, перейдите по указанной выше ссылке — Я задам кинематическую вязкость и эквивалентную шероховатость самостоятельно.
Для получения результата необходимо правильно заполнить форму и нажать кнопку рассчитать. В ходе расчета значения всех величин переводятся в систему СИ. При необходимости полученную величину потерь напора можно перевести в потери давления.
Порядок расчета потерь напора
- Вычисляются значения:
- средней скорости потока
 где Q — расход жидкости через трубопровод, A — площадь живого сечения, A=πd 2 /4, d — внутренний диаметр трубы, м
где Q — расход жидкости через трубопровод, A — площадь живого сечения, A=πd 2 /4, d — внутренний диаметр трубы, м - числа Рейнольдса — Re
 где V — средняя скорость течения жидкости, м/с, d — диаметр живого сечения, м, ν — кинематический коэффициент вязкости, кв.м/с, Rг — гидравлический радиус, для круглой трубы Rг=d/4, d — внутренний диаметр трубы, м
где V — средняя скорость течения жидкости, м/с, d — диаметр живого сечения, м, ν — кинематический коэффициент вязкости, кв.м/с, Rг — гидравлический радиус, для круглой трубы Rг=d/4, d — внутренний диаметр трубы, м
Определяется режим течения жидкости и выбирается формула для определения коэффициента гидравлического трения.
- Для ламинарного течения Re

- Для переходного режима 2000

- Для турбулентного течения Re>4000 универсальная формула Альтшуля. где к=Δ/d, Δ — абсолютная эквивалентная шероховатость.
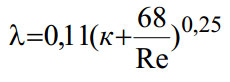
Потери напора по длине трубопровода вычисляются по формуле Дарси — Вейсбаха.
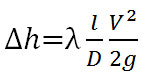
Потери напора и давления связаны зависимостью.
Потери давления по длине можно вычислить используя формулу Дарси — Вейсбаха.
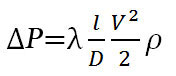
После получения результатов рекомендуется провести проверочные расчеты. Администрация сайта за результаты онлайн расчетов ответственности не несет.
Как правильно заполнить форму
Правильность заполнения формы определяет верность конечного результата. Заполните все поля, учитывая указанные единицы измерения. Для ввода чисел с десятичной частью используйте точки.
Расчет потерь напора в трубопроводах
В процессе течения нефтепродуктов имеют место потери напора на трение hτ и местные сопротивления hMC.
Потери напора на трение
Потери напора на трение при течении ньютоновских жидкостей в круглых трубах определяются по формуле Дарси—Вейсбаха
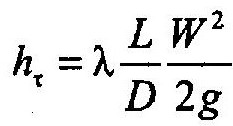
где λ — коэффициент гидравлического сопротивления; L, D — соответственно длина и внутренний диаметр трубопровода; W — средняя скорость перекачки; g — ускорение силы тяжести.
Величина коэффициента гидравлического сопротивления λ в общем случае зависит от числа Рейнольдса Re = W • D/v и относительной шероховатости труб ε = kэ/D (здесь v — кинематическая вязкость нефтепродукта при температуре перекачки; кэ — эквивалентная шероховатость стенки трубы).
При ламинарном режиме перекачки (Re = ReKp) расчет λ выполняется по формуле Стокса
В переходной зоне (ReKp -4
Эквивалентная шероховатость kэ стальных труб
С незначительной коррозией после очистки
После нескольких лет эксплуатации
Сильно заржавленные или с большими отложениями
В зоне гидравлически гладких труб турбулентного режима (ReKp ReII) расчет λ обычно ведут по формуле Шифринсона
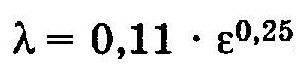
Нетрудно видеть, что формулы Стокса, Блазиуса и Шифринсона могут быть представлены зависимостью одного вида
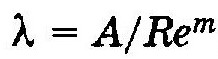
где А, т — коэффициенты, величина которых для каждой зоны трения неизменна.
Однако формула Альтшуля к этому виду не приводится. Это исключает возможность решения гидравлических задач в общем виде.
Ту же задачу можно было решить следующим образом. При Re = ReI еще справедлива формула Блазиуса, а при Re = RеI уже можно пользоваться формулой Шифринсона. Учитывая, что переходные числа Рейнольдса Альтшулем рекомендовано находить по формулам:
для зоны смешанного трения получаем:
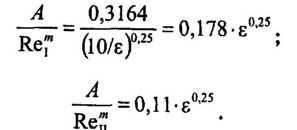
Поделив почленно получим:
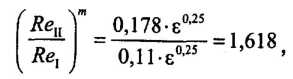
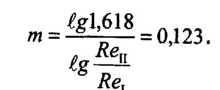
Различие в выражениях для расчета коэффициента А объясняется тем, что в первом случае не было сделано необходимое алгебраическое преобразование
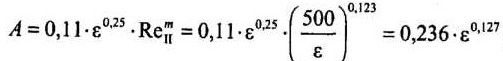
Среднеквадратичная погрешность аппроксимации В.ДБелоусова по сравнению с формулой Альтшуля составляет около 5%. Связано это, в частности, с тем, что ее автор не стремился сделать погрешность вычислений минимальной, а исходил из условия равенства коэффициентов X на границах зоны смешанного трения и соседних зон.
Автору совместно с аспиранткой Н.В. Морозовой удалось свести уравнение Альтшуля к виду со среднеквадратичной погрешностью 2,6%. Это было сделано следующим образом.
Представим формулу Альтшуля в виде
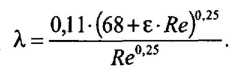
Недостатком данной записи является то, что расчетный коэффициент 0,11(68 + ε · Re) °- 25 является функцией числа Рейнольдса. Вместе с тем из формул следует, что в зоне смешанного трения справедливо неравенство
10 0 ’ 26 , а затем, используя метод наименьших квадратов, заново описали полученные точки выражением 0,206( ε · Re) 0 ’ 15 .
Подставив его получили искомую зависимость
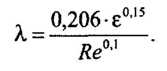
Из нее видно, что в зоне смешанного трения турбулентного режима величины коэффициентов А и т равны 0,206 • е 0,15 и 0,1 соответственно. Среднеквадратичная погрешность расчетов по формуле относительно формулы Альтшуля — менее 3%, что меньше, чем по другим известным аппроксимациям.
Следует подчеркнуть, что учет наличия переходной зоны приводит к изменению критического числа Рейнольдса. Кроме того, А.Д. Альтшуль, строго говоря, для переходных чисел Рейнольдса рекомендует диапазоны
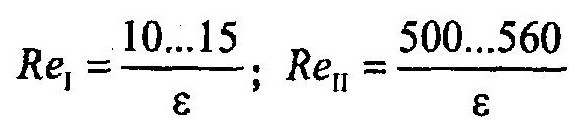
Чтобы уточнить величины Re кр , ReI ReII и найти величину Re.x,, воспользуемся следующим способом. При Re = ReKp еще справедлива формула Стокса» но в то же время уже справедлива формула Гипротрубопровода. То есть можно составить уравнение
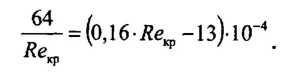
Освобождаясь от знаменателя, получаем квадратное уравнение 0,16-10 -4 · Reкр-13 · 10 -4 · Reкp-64 = 0, единственным положительным корнем которого является Reкp
Рассуждая аналогично, можно найти все остальные характерные числа Рейнольдса. Приравняв формулы Гипротрубопровода и Блазиуса, получаем Reкp = 2800. Из равенства правых частей формулы Блазиуса и формулы находим, что ReI = 17,5/ε. Наконец, приравняв правые части формулы и формулы Шифринсона, несложно найти, что ReII = 531/ε.
В тех случаях, когда необходимо, чтобы зависимость потерь напора на трение от расхода Q была выражена в явном виде, удобно использовать обобщенную формулу Лейбензона
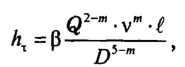
где β — расчетный коэффициент, равный
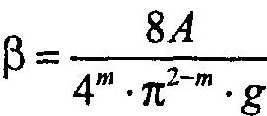
Формула получается подстановкой выражения в формулу Дарси—Вейсбаха .
Учитывая, что формулу Гипротрубопровода можно привести к виду
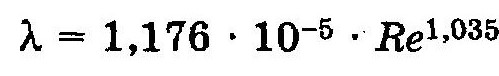
Рекомендуемые величины коэффициентов А, β и m
Расчет гидравлических потерь давления в трубопроводе из пластмасс
Расчет гидравлических потерь давления в трубопроводе из пластмасс
Гидравлический расчет является важной составляющей процесса выбора типоразмера трубы для строительства трубопровода. В нормативной литературе по проектированию этот ясный с точки зрения физики вопрос основательно запутан. На наш взгляд, это связано с попыткой описать все варианты расчета коэффициента трения, зависящего от режима течения, типа жидкости и ее температуры, а также от шероховатости трубы, одним (на все случаи) уравнением с вариацией его параметров и введением всевозможных поправочных коэффициентов. При этом краткость изложения, присущая нормативному документу, делает выбор величин этих коэффициентов в значительной степени произвольным и чаще всего заканчивается номограммами, кочующими из одного документа в другой.
С целью более подробного анализа предлагаемых в документах методов расчета представляется полезным вернуться к исходным уравнениям классической гидродинамики (1).
Потеря напора, связанная с преодолением сил трения при течении жидкости в трубе, определяется уравнением: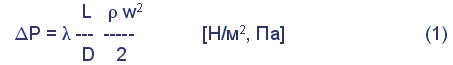
где: L и D длина трубопровода и его внутренний диаметр, м; ? — плотность жидкости, кг/м 3 ; w – средняя объемная скорость, м/сек, определяемая по расходу Q, м 3 /сек: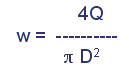
λ – коэффициент гидравлического трения, безразмерная величина, характеризующая соотношение сил трения и инерции, и именно ее определение и есть предмет гидравлического расчета трубопровода. Коэффициент трения зависит от режима течения, и для ламинарного и турбулентного потока определяется по-разному.
Для ламинарного (чисто вязкого режима течения) коэффициент трения определяется теоретически в соответствии с уравнением Пуазейля:
λ = 64/Re (2)
где: Re – критерий (число) Рейнольдса.
Опытные данные строго подчиняются этому закону в пределах значений Рейнольдса ниже критического (Re 100000 предложено много расчетных формул, но практически все они дают один и тот же результат [1 — 3].
На рис.1 показано, как «работают» уравнения (2) – (4) в указанном диапазоне чисел Рейнольдса, который достаточен для описания всех реальных случаев течения жидкости в гидравлически гладких трубах.
Рис. 1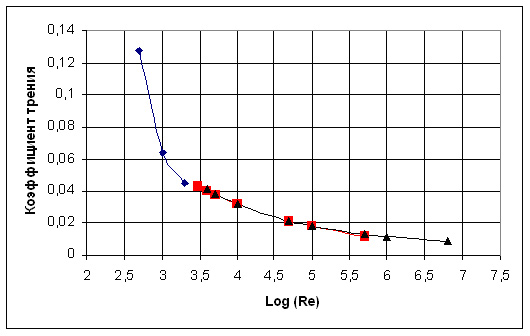
Шероховатость стенки трубы влияет на гидравлическое сопротивление только при турбулентном потоке, но и в этом случае, из-за наличия ламинарного пограничного слоя существенно сказывается только при числах Рейнольдса, превышающих некоторое значение, зависящее от относительной шероховатости ξ/D, где ξ – расчетная высота бугорков шероховатости, м.
Труба, для которой при течении жидкости выполняется условие:
считается гидравлически гладкой, и коэффициент трения определяется по уравнениям (2) – (4).
Для чисел Re больше определенных неравенством (5) коэффициент трения становится величиной постоянной и определяется только относительной шероховатостью по уравнению: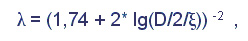
которое после преобразования дает: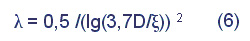
Гидравлическое понятие шероховатости не имеет ничего общего с геометрией внутренней поверхности трубы, которую можно было бы инструментально промерить. Исследователи наносили на внутреннюю поверхность модельных труб четко воспроизводимую и измеряемую зернистость, и сравнивали коэффициент трения для модельных и реальных технических труб в одних и тех же режимах течения. Этим определяли диапазон эквивалентной гидравлической шероховатости, которую следует принимать при гидравлических расчетах технических труб. Поэтому уравнение (6) точнее следует записать: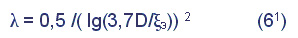
где: ξ э — нормативная эквивалентная шероховатость (Таблица 1).
Потери напора в трубопроводе;
Сайт СТУДОПЕДИЯ проводит ОПРОС! Прими участие 🙂 — нам важно ваше мнение.
При перекачке нефти по магистральному нефтепроводу напор, развиваемый насосами перекачивающих станций, расходуется на трение жидкости о стенку трубы ht, преодоление местных сопротивлений hмс, статического сопротивления из-за разности геодезических (нивелирных) отметок Dz, а также создания требуемого остаточного напора в конце трубопровода hост.
Полные потери напора в трубопроводе составят
Следует отметить, что по нормам проектирования расстояния между линейными задвижками составляют 15…20 км, а повороты и изгибы трубопровода плавные, поэтому доля местных сопротивлений невелика. С учетом многолетнего опыта эксплуатации трубопроводов с достаточной для практических расчетов точностью можно принять, что потери напора на местные сопротивления составляют 1…3% от линейных потерь. Тогда выражение (1.10) примет вид
Под разностью геодезических отметок понимают разность отметок конца и начала трубопровода Dz = zк – zн . Величина Dz может быть как положительной (перекачка на подъем), так и отрицательной (под уклон).
Остаточный напор hост необходим для преодоления сопротивления технологических коммуникаций и заполнения резервуаров конечного пункта (а также промежуточных перекачивающих станций, находящихся на границе эксплуатационных участков).
Потери напора на трение в трубопроводе определяют по формуле Дарси-Вейсбаха
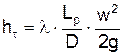 , (1.12)
, (1.12)
либо по обобщенной формуле лейбензона
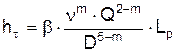 , (1.13)
, (1.13)
где Lр – расчетная длина нефтепровода;
D – внутренний диаметр трубы;
w – средняя скорость течения нефти по трубопроводу;
Q – расход нефти.
n – расчетная кинематическая вязкость нефти;
l – коэффициент гидравлического сопротивления;
b, m – коэффициенты обобщенной формулы Лейбензона.
Значения l, b и m зависят от режима течения жидкости и шероховатости внутренней поверхности трубы. Режим течения жидкости характеризуется безразмерным параметром Рейнольдса
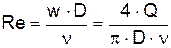 , (1.14)
, (1.14)
При значениях Re Re2.
Значения переходных чисел Рейнольдса Re1 и Re2 определяют по формулам
 ,
,
где 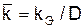 – относительная шероховатость трубы;
– относительная шероховатость трубы;
kЭ – эквивалентная (абсолютная) шероховатость стенки трубы, зависящая от материала и способа изготовления трубы, а также от ее состояния. Для нефтепроводов после нескольких лет эксплуатации можно принять kЭ=0,2 мм.
Расчет коэффициентов l, b и m выполняется по формулам, приведенным в табл. 1.5.
Таблица 1.5 – Значения коэффициентов l, b и m для различных


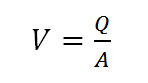 где Q — расход жидкости через трубопровод, A — площадь живого сечения, A=πd 2 /4, d — внутренний диаметр трубы, м
где Q — расход жидкости через трубопровод, A — площадь живого сечения, A=πd 2 /4, d — внутренний диаметр трубы, м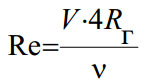 где V — средняя скорость течения жидкости, м/с, d — диаметр живого сечения, м, ν — кинематический коэффициент вязкости, кв.м/с, Rг — гидравлический радиус, для круглой трубы Rг=d/4, d — внутренний диаметр трубы, м
где V — средняя скорость течения жидкости, м/с, d — диаметр живого сечения, м, ν — кинематический коэффициент вязкости, кв.м/с, Rг — гидравлический радиус, для круглой трубы Rг=d/4, d — внутренний диаметр трубы, м