3 х 2 1 х 3 производная

Онлайн вычисление производных

Вычислить производную онлайн нa matematikam.ru — быстро, надежно, точно и абсолютно бесплатно! Нахождение производной функции первого, второго и т.д. порядка дифференцирования. Введите нужную функцию — и вы тут же получите онлайн решение производной.

Вычислить производную онлайн

Данный калькулятор по расчету производных онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!

Вычислить производную онлайн

Производная

Вычисление производной от математической функции (дифференцирование) является очень частой задачей при решении высшей математики. Для простых (элементарных) математических функций это является довольно простым делом, поскольку уже давно составлены и легко доступны таблицы производных для элементарных функций. Однако, нахождение производной сложной математической функции не является тривиальной задачей и часто требует значительных усилий и временных затрат.

Найти производную онлайн

Наш онлайн сервис позволяет избавиться от бессмысленных долгих вычислений и найти производную онлайн за одно мгновение. Причем воспользовавшись нашим сервисом, расположенным на сайте www.matematikam.ru, вы можете вычислить производную онлайн как от элементарной функции, так и от очень сложной, не имеющей решения в аналитическом виде. Главными преимуществами нашего сайта по сравнению с другими являются: 1) нет жестких требований к способу ввода математической функции для вычисления производной (например при вводе функции синус икс вы можете ввести ее как sin x либо sin(x) либо sin[x] и т.д.); 2) вычисление производной онлайн происходит мгновенно в режиме онлайн и абсолютно бесплатно; 3) мы позволяем находить производную от функции любого порядка, изменить порядок производной очень легко и понятно; 4) мы позволяем найти производную почти от любой математической функции онлайн, даже очень сложной, недоступной для решения другими сервисами. Выдаваемый ответ всегда точен и не может содержать ошибки.

Использование нашего сервера позволит вам 1) вычислить производную онлайн за вас, избавив от длительных и утомительных вычислений, в ходе которых вы могли бы допустить ошибку или опечатку; 2) если вы вычисляете производную математической функции самостоятельно, то мы предоставляем вам возможность сравнить полученный результат с вычислениями нашего сервиса и убедиться в верности решения либо отыскать закравшуюся ошибку; 3)пользоваться нашим сервисом вместо использования таблиц производных простых функций, где зачастую необходимо время для нахождения нужной функции.

Всё что от вас требуется, чтобы найти производную онлайн — это воспользоваться нашим сервисом на онлайн решение производной, ввести заданную функцию, выбрать порядок производной и получить ответ. Приятного вам пользования.

Как найти производную? Помогите решить 1 вариант

Производная есть предел отношения изменения функции к изменению аргумента при том, что последний стремится к нулю.

Изменение аргумента, то есть Δx это х-x₀. (1)

Изменение функции, то есть Δf это f(х)-f(х₀). (2)

При этом х=x₀+Δx, что можно увидеть из (1)

Для примера, пусть наша функция: f(х)=3x²-5x+7. Нужно найти производную

Наша задача: выразить всё через x₀ и Δx.

Приведём подобные, получим:

Δf = 6x₀Δx + 3Δx² + 5Δx

Обратим внимание, что в нашем выражении мы можем вынести Δx как общий множитель:

Δf = Δx(6x₀ + 3Δx + 5)

Напомню, что производная это предел отношения:

Так что внутри предела мы сокращаем Δx.

Остаётся выражение: 6x₀ + 3Δx + 5

Если мы учтём, что Δx->0, то получим, что

В общем виде записывают просто х. То есть

f'(x) — обозначение производной.

Есть также гораздо более простой способ нахождения производной: по таблице. Прикрепил её ниже:

Если вам интересно, как искать производные по таблице (это совсем-совсем несложно), и если вы не стесняетесь матов в тексте, могу предложить вам посетить мою группу ВКонтакте, там я в статьях как раз разбирал этот материал.

Помогите решить. Пожалуйста.

Как вы объясните маленькому ребенку, что такое производная и интеграл?

Проще всего на примере физического смысла. Вот есть машина, она начинает ехать, разгоняясь, потом ускоряясь еще быстрее, потом замедляясь, потом водитель по тормозам ударил со всей мочи, потом педаль в пол втопил. Производная покажет, как менялась скорость машины. Где водитель разгонялся постепенно, где разгонялся быстро, где тормозил потихоньку, где резко. Интеграл покажет, какой путь он проехал за время движения.

Можете помочь вычислить производную функции y = x+siny=e^(x-y)?

Что-то непонятное условие. Как там может быть два знака равенства? Не опечатка ли? Это очень странно и непонятно что вообще значит. Если бы только один, тогда можно было бы что-то с неявной функцией сделать

Математика-это «точная наука» ?

Математика — это наука об объективных свойствах идеализированных объектов. Поскольку объекты идеальны, а не реальны, то их основные свойства известны априори (в форме аксиом), а сама математика — это самая точная наука из всех.

С другой стороны, идеализированные объекты не существуют в реальной действительности. Поэтому математика не является ни естественной наукой (как физика — естественная и довольно «точная», или палеонтология — естественная, но довольно «неточная» уже просто в силу принципиальной неполноты доступной информации), ни гуманитарной (где тоже есть науки «точные» и «неточные»). В этом отношении математика — наука совершенно особая, но ее инструментарий можно применять в любых иных науках, чьи объекты позволяют себя так или иначе идеализировать и количественно описывать. И именно возможность и полнота количественного описания объектов с применением средств математики характеризует «точность» других наук.

В комментариях к вопросу оспаривалась сама возможность причисления математики к «науке». Но идеализированность объекта изучения не лишает его объективных свойств и не исключает ошибок исследователя. Разница с естественными науками лишь в том, что место экспериментов и измерений занимают доказательства и расчеты. Которые вполне могут быть ошибочны (аналог плохо поставленного эксперимента). Идеализированность, в общем случае, даже не гарантирует принципиальную возможность обретения полного знания о изучаемых объектах. Наоборот, доказано, что это знание не всегда может быть полным.

Что такое корень уравнения?

Корень уравнения — это число, которое можно подставить в уравнение вместо переменной (обычно x или y) и получить в итоге одинаковые значения выражений по обе стороны знака равно.

Например, если в уравнение 2x+1=x+4 подставить вместо x число 3, то по обе стороны знака равно получим число 7.

Получается, что корнем данного уравнения будет число 3.

Важно понимать, что корнем является не сама переменная x, а число 3!

Помогите решить задачу по теоретической физике?

Два одинаковых жестких стержня длины R имеют общую точку подвеса O. Стержни могут вращаться в вертикальной плоскости вокруг точки подвеса независимо друг от друга. К концам стержней прикреплены два одинаковых груза А и В массы т каждый, соединенные между собой пружиной жесткости c. Длина пружины в состоянии устойчивого равновесия системы равна l. Пренебрегая массой стержней, найти частоты главных колебаний около устойчивого положения равновесия грузов.

Я плохо представляю себе, как эти рычаги размещены и движутся друг относительно друга. (А уж техническую реализацию вообще не представляю.) И в одной ли вертикальной плоскости они движутся (ну, наверное), или в двух разных (тогда данных, вроде, маловато). Поэтому решать не берусь. Да и лень. Но общая идея такова…

Закрепленные на рычагах массы имеют по одной степени свободы и, соответственно, положение каждой описывается одной обобщенной координатой. А именно, массы способны вращаться по вертикальному кругу, радиусом в длину их рычага, с центром в точке крепления рычагов. Ну а наиболее удобная обобщенная координата — это угол поворота по этому самому кругу.

Система в целом имеет две степени свободы (1+1) и две обобщенные координаты (угол для первой массы и угол для второй).

Скорость вращения каждой из масс равна длине рычага, умноженной на первую производную обобщенной координаты (производную от угла) по времени. Далее, зная скорости и массы, находим полную кинетическую энергию системы — как сумму кинетических энергий двух вращающихся масс.

Далее, находим потенциальную энергию каждой массы в гравитационном поле Земли как mgh, где m — масса, g — ускорение свободного падения, а h — высота. h зависит от обобщенной координаты (угла) для данной массы как сумма некоей константы и произведения длины рычага на некую тригонометрическую функцию от обобщенной координаты. Константа нам неинтересна (обратится в ноль при дифференцировании) и можно ее просто положить равной нулю (так мы выбрали точку отсчета высоты). А тригонометрическую функцию можно представить в виде косинуса от некоего постоянного угла, ± обобщенная координата. Можно так выбрать обобщенную координату, что будет просто косинус от нее. Для этого коорлината должна обращаться в ноль в самой верхней точке и в ±π — в самой нижней.

Кроме двух потенциальных энергий двух масс, имеем еще и потенциальную энергию упругой деформации пружины. Эта энергия равна произведению расстояния между массами, умножить на коэффициент упругости. Расстояние выражаем через обе обобщенные координаты, учитывая геометрию системы в целом (как уже писал, мне не вполне понятную по описанию). Если оба рычага вращаются по одному кругу (в одной и той же плоскости), то расстояние между массами найти легко. Если плоскости вращения разные, то нужно знать их взаимную ориентацию. То есть, еще и угол между ними. Но, как бы там ни было, а считается, что взаимное расстояние вы можете выразить через две обобщенные координаты системы.

Далее, суммируем все три потенциальные энергии, вычитаем их сумму из кинетической и, тем самым, находим лагранжиан. Лагранжиан засовываем в уравнения Лагранжа: https://ru.wikipedia.org/wiki/Уравнения_Лагранжа_второго_рода . Получаем из них систему двух дифуров для двух обобщенных координат.

Поскольку приказано решать задачу «около устойчивого положения равновесия», то именно около него и решаете. Это значит, например, что можно пренебречь квадратичными отклонениями обобщенных координат от из равновесных значений. Вероятно, это должно сделать систему дифуров линейной «около устойчивого положения равновесия». И, в частности, позволяет
разложить тригонометрические функции в ряд по отклонениям от равновесия и отбросить все слагаемые ряда, кроме нулевой и первой степени.

Еще можно вспомнить, что равновесие — это когда равна нулю сумма всех сил. Имея дело с лагранжианом, удобно пользоваться «обобщенными» силами. В отсутствие непотенциальных сил, обобщенная сила обратится в ноль при равенстве нулю обобщенного градиента от лагранжиана. Иными словами, в равновесии равны нулю обе частные производные от лагранжиана по каждой из обобщенных координат. Эти два уравнения должны, вероятно, помочь вам найти равновесные значения обобщенных координат, квадратичными отклонениями от которых мы пренебрегаем.

Ну, вот… Есть линеаризованная система двух дифуров для двух неизвестных (в роли неизвестных уже не сами обобщенные координаты, а их отклонения от равновесных значений).Из дифуров находите две собственные частоты системы.

3 х 2 1 х 3 производная

• +7 (953) 35-222-89
• Санкт-Петербург, Лиговский пр.52
• [email protected]

Производная, часть II: геометрический смысл

Продолжение задач на производные для первой части ЕГЭ.

Геометрический смысл производной и ее применения для исследования функций.

Геометрический смысл производной

Про геометрический смысл написано много теории. Не буду вдаваться в вывод приращения функции, напомню основное для выполнения заданий:

Производная в точке x равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, то есть это тангенс угла наклона к оси Х.

Возьмем сразу задание из ЕГЭ и начнем в нем разбираться:

Задание №1. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
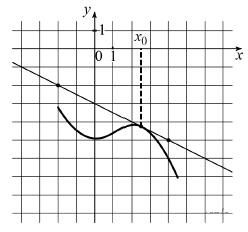Кто очень торопится и не хочет разбираться в объяснениях: стройте до любого такого треугольника (как показано ниже) и делите стоячую сторону (вертикальную) на лежащую (горизонтальную) и будет вам счастье, если про знак не забудите (если прямая убывает(→↓), то ответ должен быть с минусом, если прямая возрастает(→↑), то ответ должен быть положительный!)

Найти нужно угол между касательной и осью Х, назовем его α: проведем параллельную оси Х прямую в любом месте через касательную к графику, получим тот же угол.

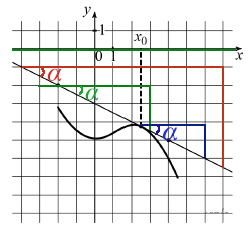
Лучше не брать точку х0, т.к. понадобится большая лупа для определения точных координат.

Взяв любой прямоугольный треугольник (на рисунке предложено 3 варианта), найдем tgα (углы, то равны, как соответственные), т.е. получим производную функции f(x) в точке x0. Почему же так?

Если мы проведем касательные в других точках x2, x1 и т.д. касательные будут другие.

Вернемся к 7 классу, чтобы построить прямую!

Уравнение прямой задается уравнением y = kx + b , где

k — наклон относительно оси Х.

b — расстояние между точкой пересечения с осью Y и началом координат.

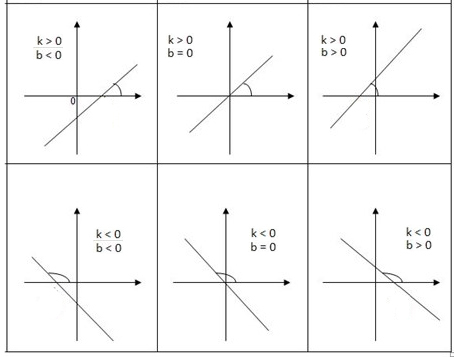
Производная прямой, всегда одна и та же: y’ = k.

В какой бы точке на прямой мы не взяли производную, она будет неизменна.

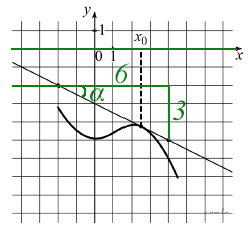
Поэтому, осталось только найти tgα (как было сказано выше: делим стоячую сторону на лежачую). Делим противолежащий катет на прилежащий, получаем, что k = 0,5. Однако, если график убывает, коэффициент отрицательный: k = −0,5.

Советую себя проверять вторым способом:
По двум точкам можно задать прямую. Найдем координаты двух любых точек. Например, (-2;-2) и (2;-4):

Подставим в уравнение y = kx + b вместо y и х координаты точек:

Решив эту систему, получим b = −3, k = −0,5

Вывод: Второй способ дольше, но в нем вы не забудете про знак.

Задание №2 . На рисунке изображён график производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, . x8. Сколько из этих точек лежит на промежутках возрастания функции f(x) ?

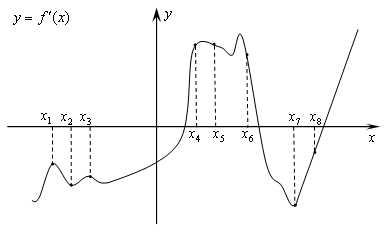
Если график функции убывает — производная отрицательна (верно и наоборот).

Если график функции возрастает — производная положительна (верно и наоборот).

Эти две фразы помогут вам решить большую часть задач.

Внимательно смотрите, рисунок производной вам дан или функции, а дальше выбирайте одну из двух фраз.

Построим схематично график функции. Т.к. нам дан график производной, то там, где она отрицательна, график функции убывает, где положительна — возрастает!

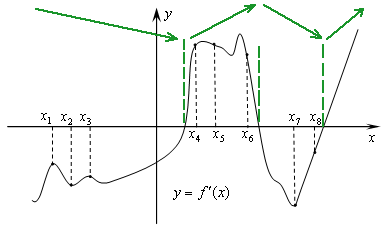
Получается, что 3 точки лежат на участках возрастания: x4; x5; x6.

Задание №3. Функция f(x) определена на промежутке (-6; 4). На рисунке изображен график ее производной . Найдите абсциссу точки, в которой функция принимает наибольшее значение.

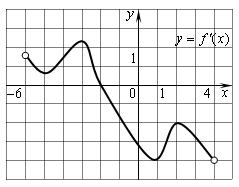
Советую всегда строить, как идет график функции, такими стрелочками или схематично со знаками (как в №4 и №5):

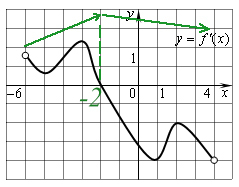
Очевидно, если график возрастает до −2, то максимальная точка и есть −2.

Задача №4. На рисунке изображён график функции f(x) и двенадцать точек на оси абсцисс: x1, x2, . x12. В скольких из этих точек производная функции отрицательна?

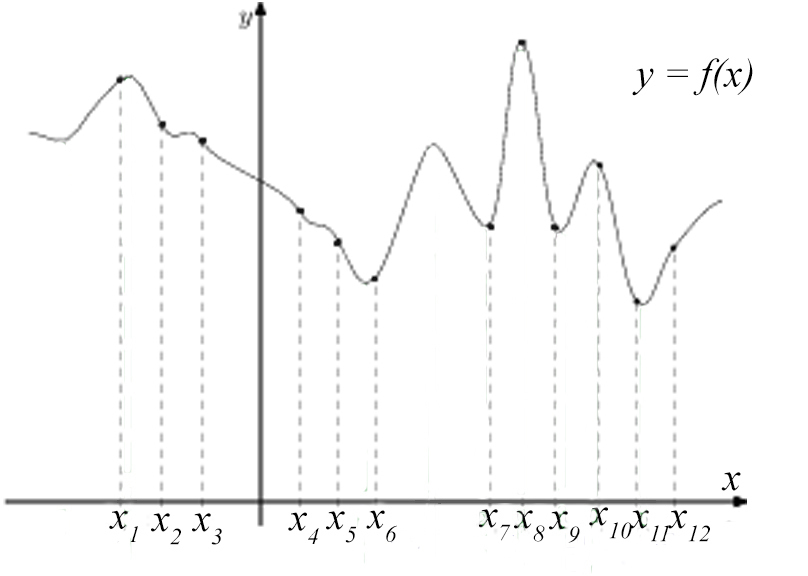
Задача обратная, дан график функции, нужно схематично построить, как будет выглядеть график производной функции, и посчитать, сколько точек будет лежать в отрицательном диапазоне.

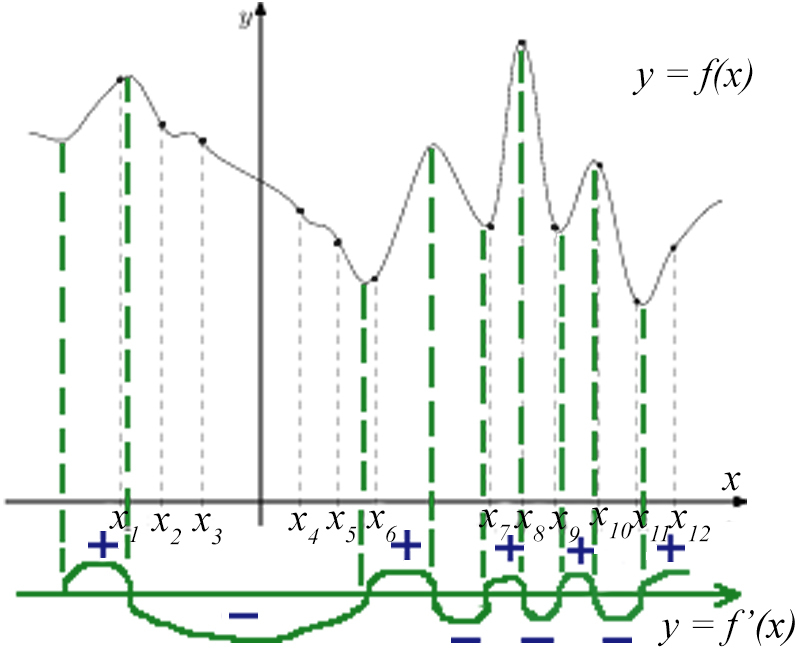
Положительные: x1, x6, x7, x12.

Отрицательные: x2, x3, x4, x5, x9, x10, x11.

Ответ: 7

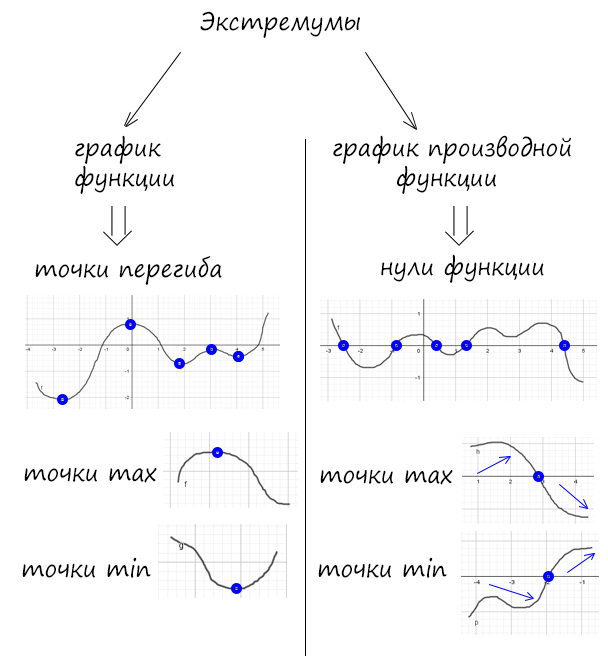
Еще один вид заданий, когда спрашивается про какие-то страшные «экстремумы»? Что это такое вам найти не составит труда, я же поясню для графиков.

Задача №5. На рисунке изображен график производной функции f(x), определенной на интервале (-16; 6). Найдите количество точек экстремума функции f(x) на отрезке [-11; 5].

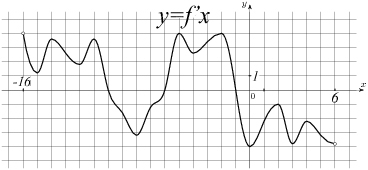Отметим промежуток от -11 до 5!

Обратим свои светлые очи на табличку: дан график производной функции => тогда экстремумы это точки пересечения с осью X.

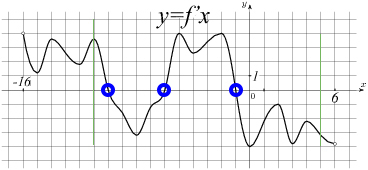
Задача №6. На рисунке изображен график производной функции f(x), определенной на интервале (-13; 9). Найдите количество точек максимума функции f(x) на отрезке [-12; 5].

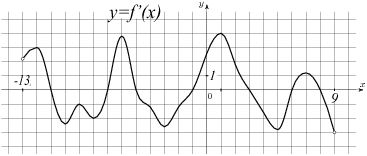Отметим промежуток от -12 до 5!

Можно одним глазом взглянуть в табличку, точка максимума — это экстремум, такой, что до него производная положительна (функция возрастает), а после него производная отрицательна (функция убывает). Такие точки обведены в кружочек.

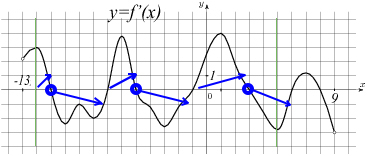
Стрелочками показано, как ведет себя график функции

Задача №7. На рисунке изображен график функции f(x),определенной на интервале (-7; 5). Найдите количество точек, в которых производная функции f(x) равна 0.

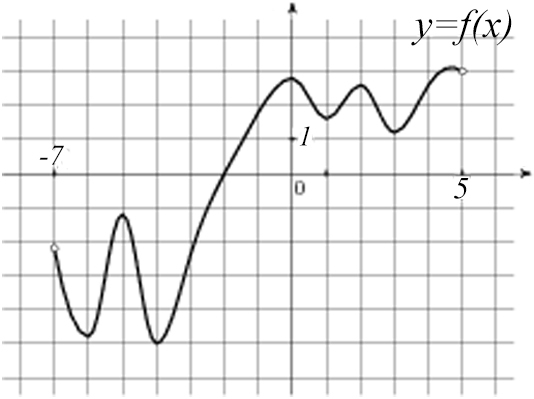
Можно посмотреть на выше приведенную табличку (производная равна нулю, значит это точки экстремума). А в даной задаче дан график функции, значит требуется найти количество точек перегиба !

А можно, как обычно : строим схематический график производной.

Производная равна нулю, когда график функций меняет свое направление (с возрастания на убывание и наоборот)

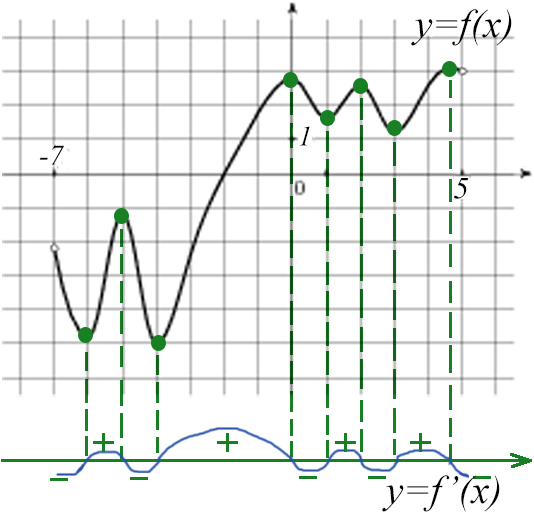
Задача №8. На рисунке изображен график производной функции f(x), определенной на интервале (-2; 10). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

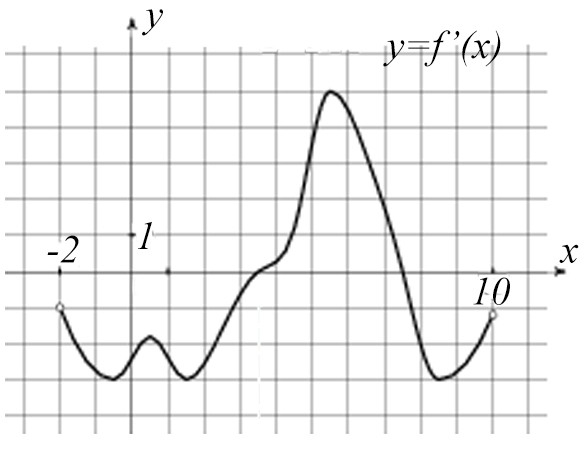
Построим схематично график функции:

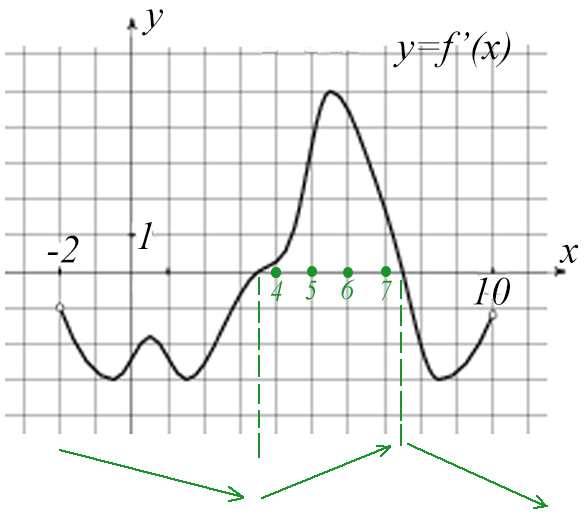
Там, где он возрастает, получаем 4 целые точки: 4 + 5 + 6 + 7 = 22.

Задача №9. На рисунке изображен график производной функции f(x), определенной на интервале (-6; 6). Найдите количество точек f(x), в которых касательная к графику функции параллельна прямой y = 2x + 13 или совпадает с ней.

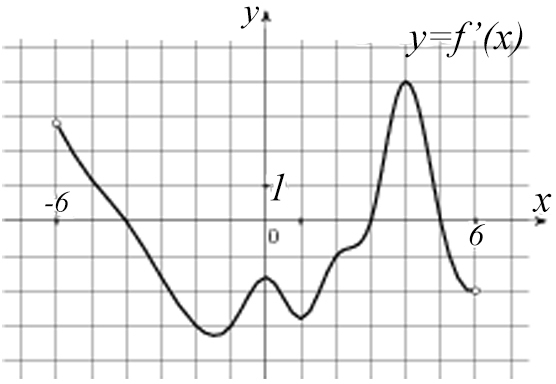
Нам дан график производной! Значит, и нашу касательную нужно «перевести» в производную.

Производная касательной: y’ = 2.

А теперь построим обе производные:

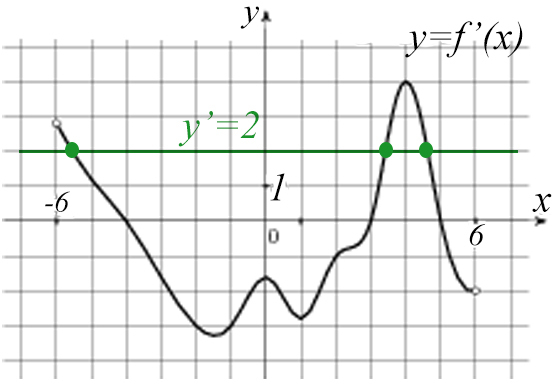Касательные пересекаются в трех точках, значит, наш ответ 3.

Задача №10. На рисунке изображен график функции f(x), и отмечены точки -2, 1, 2, 3. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

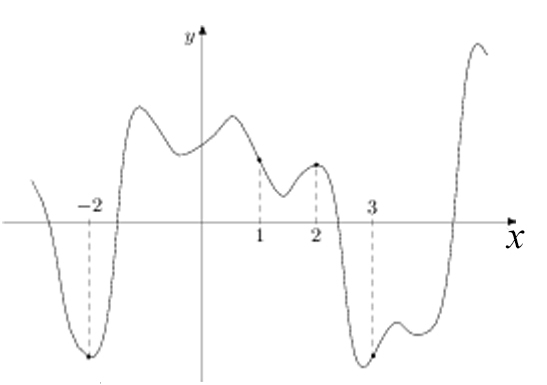
Задание чем-то похоже на первое: чтобы найти значение производной, нужно построить касательную к этому графику в точке и найти коэффициент k.

Если прямая убывает, k 0.

Подумаем, как значение коэффициента отразится на наклоне прямой:

При k = 1 или k = − 1 график будет посередине между осями Х и У.

Чем ближе прямая к оси Х, тем ближе коэффициент k нулю.

Чем ближе прямая к оси Y, тем ближе коэффициент k к бесконечности.

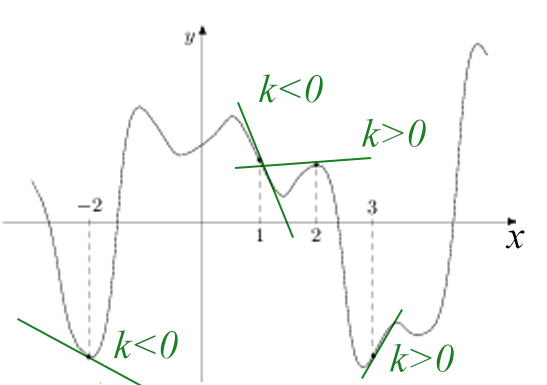
В точке -2 и 1 k именно там и будет наименьшее значение производной

Задание №11. Прямая является касательной y = 3x + 9 к графику функции y = x³ + x² + 2x + 8 . Найдите абсциссу точки касания.

Прямая будет касательной к графику, когда графики имеют общую точку, как и их производные. Приравняем уравнения графиков и их производные:

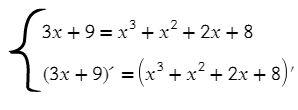Решив второе уравнение, получаем 2 точки. Чтобы проверить, какая из них подходит, подставляем в первое уравнение каждый из иксов. Подойдет только один.

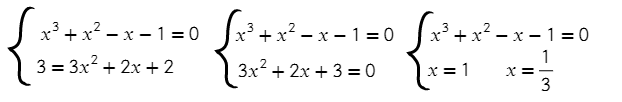
Кубическое уравнение совсем решать не хочется, а квадратное за милую душу.

Вот только, что записывать в ответ, если получится два «нормальных» ответа?

При подстановке икса (х) в первоначальные графики y = 3x + 9 и y = x³ + x² + 2x + 8 должен получиться один и тот же Y

Верно! Значит x=1 и будет ответом

Задание №12. Прямая y = − 5x − 6 является касательной к графику функции ax² + 5x − 5 . Найдите a .

Аналогично приравняем функции и их проивзодные:

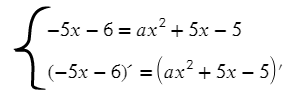
Решим эту систему относительно переменных a и x :

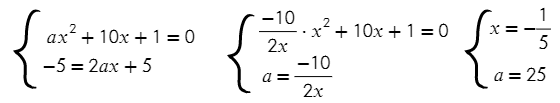Ответ: 25

Задание с производными считается одним из самых сложных в первой части ЕГЭ, однако, при небольшой доли внимательности и понимания вопроса у вас все получится, и вы поднимете процент выполнения этого задания!

Большинство заданий взято с сайтов ФИПИ и РЕШУ ЕГЭ.

3 х 2 1 х 3 производная

ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ X

§ 231. Понятие о второй производной. Производные высших порядков

Производная от производной у’ функции у называется второй производной этой функции и обозначается у» или f»(х):

Рассмотрим несколько примеров.

По правилу дифференцирования многочленов

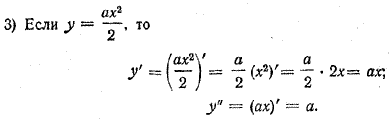
Вторая производная y» функции y, так же как и первая ее производная у’, допускает простую физическую интерпретацию. Будучи производной от первой производной у’, она характеризует скорость изменения этой производной. Первая же производная у’ характеризует скорость изменения функции у. Таким образом, у» характеризует «скорость изменения скорости изменения» функции у. С подобным понятием мы уже сталкивались в физике. Изучая равноускоренное движение, мы вводили понятие ускорения как изменения скорости движения в единицу времени. Это понятие как раз и характеризует скорость изменения скорости движения. Поэтому, используя язык механики, можно сказать, что вторая производная у» функции у есть ускорение, с которым функция
у = f (х) изменяет свои значения при изменении значений аргумента х.

Третья производная функции у = f (х) есть производная от второй производной этой функции. Она обозначается у»‘ или f'»‘(x) : у'» = (у»)‘, f'»‘(x) = [f'»(x)]‘. Аналогично, четвертая производная функции у = f (х) обозначается y IV или f’ IV x) есть производная от ее третьей производной и т. д.

п-я производная функции f (х) иначе называется производной п-го порядка (обозначается f n (х)). Например, третья производная иначе называется производной третьего порядка, четвертая производная — производной четвертого порядка и т. д.

Очевидно, что все производные данной функции, начиная с третьей, равны нулю.

1836. Найти ускорение тела, движущегося по закону s (t) = 2t 3 + 5t 2 + 4t (s — путь в метрах, t — время в минутах), в момент времени: a) t = 40 сек; б) t = 1 ч.

1837. Найти ускорение тела, движущегося по закону s = √ t (s — путь в метрах, t — время в минутах), в произвольный момент времени t.

Для данных функций найти производные всех порядков (1838—1843):.

1844. Доказать, что для функции у = a sin x + b cos х справедливо соотношение y IV = у.

1845. Сколько раз нужно продифференцировать функцию у = (х 2 + 1) 100 , чтобы в результате получился многочлен 50-й степени?

1846*. Найти производную 100-го порядка от функции у = sin х cos 2 х.