Параллельное соединение участков цепи
Последовательное и параллельное соединения проводников

1. Потребители электрической энергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).
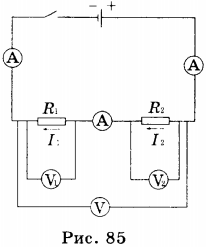
Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.
При последовательном соединении проводников ток проходит через все лампочки, при этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд, т.е. заряд не скапливается ни в какой части проводника. Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: ( I_1=I_2=I ) .
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: ( R_1=R_2=R ) . Это следует из того, что при последовательном соединении проводников их общая длина увеличивается, она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: ( U_1=IR_1 ) , ( U_2=IR_2 ) , а общее напряжение равно ( U=I(R_1+R_2) ) . Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: ( U=U_1+U_2 ) .
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
2. Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).
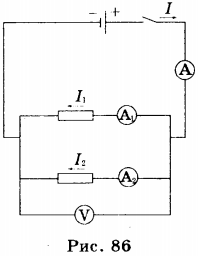
Поэтому вольтметр, подключенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким образом, напряжение на концах всех параллельно соединённых проводников одно и то же: ( U_1=U_2=U ) .
При параллельном соединении проводников электрическая цепь разветвляется, в данном случае в точке В. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: ( I=I_1+I_2 ) .
В соответствии с законом Ома ( I=frac
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление ( r ) , то их общее сопротивление равно: ( R=r/2 ) . Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения, соответственно уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно: они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них и соответствие суммарной силы тока предельно допустимой силе тока.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением ( R_1 ) и ( R_2 ) . Напряжения на резисторах соответственно ( U_1 ) и ( U_2 ) .
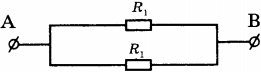
По какой из формул можно определить напряжение U на участке АВ?
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением ( R_1 ) и ( R_2 ) . Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
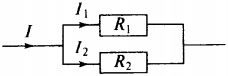
1) ( I=I_1=I_2 )
2) ( I=I_1+I_2 )
3) ( U=U_1+U_2 )
4) ( R=R_1+R_2 )
3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R> и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением ( R_1 ) и ( R_2 ) . Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением ( R_1 ) . По какой из формул можно определить общее сопротивление цепи ( R ) ?
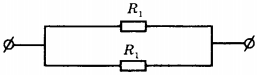
6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов ( R_1 ) и ( R_2 ) равны. Чему равно сопротивление каждого резистора?

1) 81 Ом
2) 18 Ом
3) 9 Ом
4) 4,5 Ом
7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?

1) 1/3 Ом
2) 3 Ом
3) 9 Ом
4) 27 Ом
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ( R_1 ) = 1 Ом, ( R_2 ) = 10 Ом, ( R_3 ) = 10 Ом, ( R_4 ) = 5 Ом?
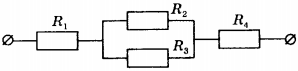
1) 9 Ом
2) 11 Ом
3) 16 Ом
4) 26 Ом
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ( R_1 ) = 1 Ом, ( R_2 ) = 3 Ом, ( R_3 ) = 10 Ом, ( R_4 ) = 10 Ом?
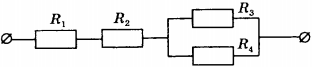
1) 9 Ом
2) 10 Ом
3) 14 Ом
4) 24 Ом
10. Если ползунок реостата (см. схему) переместить влево, то сила тока
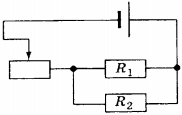
1) в резисторе ( R_1 ) уменьшится, а в резисторе ( R_2 ) увеличится
2) увеличится в обоих резисторах
3) в резисторе ( R_1 ) увеличится, а в резисторе ( R_2 ) уменьшится
4) уменьшится в обоих резисторах
11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?
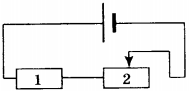
Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) сопротивление реостата 2
Б) сила тока в цепи
B) напряжение на резисторе 1
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется
12. Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении двух резисторов ( R_1 ) и ( R_2 ) . Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе ( R_1 ) и ( R_2 )
Б) напряжение на резисторе ( R_2 )
B) общее напряжение на резисторах ( R_1 ) и ( R_2 )
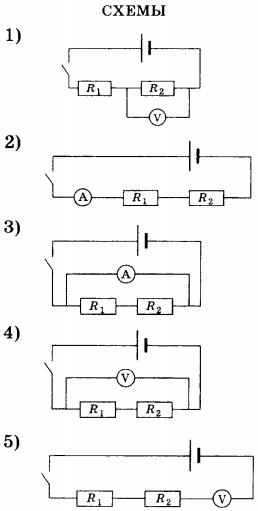
Часть 2
13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов ( R_1 ) = 10 Ом, ( R_2 ) = 5 Ом, ( R_3 ) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?
Последовательное и параллельное соединение сопротивлений
Последовательное соединение сопротивлений
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
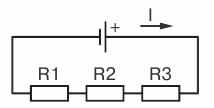
Рис 1 . Последовательное соединение сопротивлений
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U1 = IR1 U2 = IR2 и U3 = IR3
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
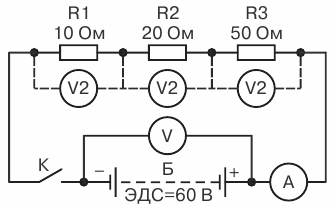
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75 х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.

Параллельное соединение сопротивлений
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
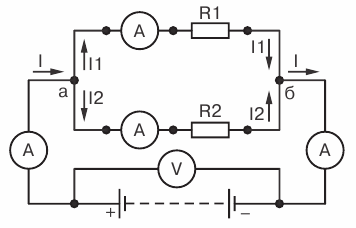
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (—), заметим, что прибор покажет ту же величину силы тока.
Значит, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R 1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U 1 — падение напряжения на сопротивлении R 1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U 1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 + I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть ( I1 = 300 мА) пошла через меньшее сопротивление ( R1 = 10 Ом), а меньшая часть ( R2 = 150 мА) — через большее сопротивление ( R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
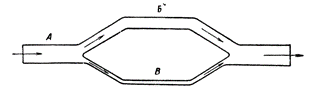
Рис. 4 . Через тонкую трубу в один и тот же промежуток времени пройдет воды меньше, чем через толстую
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U 1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.

Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).
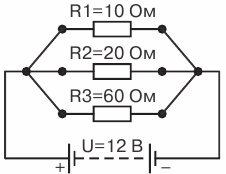
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0, 2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 = 1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / ( R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Физика. 10 класс
Конспект урока
Физика, 10 класс
Урок 29. Закон Ома для участка цепи. Соединения проводников
Перечень вопросов, рассматриваемых на уроке:
- условия, необходимые для существования электрического тока;
- постоянный электрический ток;
- закон Ома для участка цепи;
- формула расчета сопротивления проводника с учетом свойств материала проводника и его геометрических размеров;
- типы соединений проводников и формулы расчета параметров электрической цепи для каждого типа.
Глоссарий по теме.
Сила тока I — скалярная величина, равная отношению заряда q, прошедшего через поперечное сечение проводника, к промежутку времени t, в течение которого шёл ток.
Постоянный ток — электрический ток, не изменяющийся со временем.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом.
Параллельное соединение проводников. При параллельном соединении концы проводников присоединены к одной и той же паре точек.
Смешанное соединение проводников — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Узел – это точка электрической цепи, где сходится не менее трех ветвей.
Свойство проводника ограничивать силу тока в цепи, то есть противодействовать электрическому току, называют электрическим сопротивлением проводника.
Резистор или проводник — элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления.
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 335 – 340.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009. – С. 105 – 109.
3. Элементарный учебник физики. Учебное пособие в 3 томах под редакцией академика Ландсберга Г.С.: Т.2. Электричество и магнетизм. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 110 – 115.
4. Тульчинский М.Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 83 – 87.
5. Савельев И.В. Курс общей физики, том II. Электричество. М.: Изд. «Наука», 1970 г. С. 108.
Открытые электронные ресурсы:
Теоретический материал для дополнительного изучения
Сложно представить нашу жизнь без электрического тока. Каждый день, не задумываясь, мы используем различные электрические приборы, в основе работы которых лежат простые и сложные электрические цепи. Какому закону подчиняются основные параметры электрических цепей? Как рассчитать эти цепи, чтобы приборы работали исправно?
Вы уже знаете, электрическим током называют упорядоченное (направленное) движение заряженных частиц.
Для возникновения и существования электрического тока в проводнике необходимо:
- наличие свободных заряженных частиц;
- сила, действующая на них в определённом направлении, то есть наличие электрического поля в проводнике.
Различают следующие действия электрического тока:
Постоянный ток — электрический ток, у которого сила тока и направление не изменяются со временем.
Сила тока I равна отношению электрического заряда q, прошедшего через поперечное сечение проводника, ко времени его прохождения t:

За направление электрического тока условно выбрано направление движения положительно заряженных частиц, то есть в сторону, противоположную направлению движения электронов.

Для каждого проводника – твердого, жидкого и газообразного – существует определённая зависимость силы тока от приложенной разности потенциалов (напряжения) на концах проводника. Эту зависимость выражает, так называемая, вольт-амперная характеристика проводника.

Для широкого класса проводников (в т. ч. металлов ) при неизменной температуре справедлив закон Ома для участка цепи:
Сила тока на участке цепи прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению этого участка цепи:

Закон имеет простую форму, но доказать экспериментально его справедливость довольно трудно.
Закон Ома является основой всей электротехники постоянных токов. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно.
Основная электрическая характеристика проводника – сопротивление. От этой величины зависит сила тока в проводнике при заданном напряжении. Причиной электрического сопротивления является взаимодействие электронов при их движении по проводнику с ионами кристаллической решетки. Сопротивление проводника зависит от свойств материала проводника и его геометрических размеров.

Электрическое сопротивление металлов прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения:

где величина ρ – удельное сопротивление проводника — величина, зависящая от рода вещества и его состояния (от температуры в первую очередь). Удельное сопротивление веществ приводятся в справочных таблицах.
Омметр – прибор для измерения сопротивления.
От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию. Для этого составляют электрические цепи различной сложности. Различают последовательное, параллельное, смешанное соединения проводников.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. Главная особенность последовательного соединения заключается в том, что через все проводники протекает одинаковый ток. Если через один проводник протекает ток определенной величины, то такой же ток протекает и через все остальные. Если хотя бы в одном проводнике отсутствует ток, то он обязательно отсутствует и во всех остальных. Напряжение на концах последовательно соединенных проводников складывается. Полное сопротивление всего участка цепи при последовательном соединении равно сумме сопротивлений всех проводников.
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
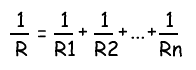
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
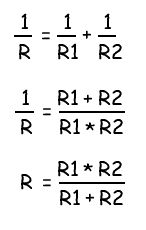
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
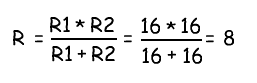
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:
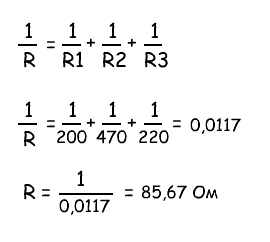
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.


