методы решения задач с параметрами

Следующая тема курса – графические методы решения задач с параметром

Существует два принципиально различных подхода – построение графиков функций или уравнений в плоскости (x; y) или в плоскости (x; a) . Кроме того, для графического метода решения задач с параметром в плоскости (x; y) необходимо рассмотреть различные виды преобразования графиков – обычно это параллельный перенос, поворот прямой и гомотетия. Есть класс задач, решение которых основано на аналитических свойствах функций (области определения, области значений, четности, периодичности и т.д.), эти свойства и приемы их использования тоже нужно знать.

На этом перечень методов решения задач с параметрами, разумеется, не заканчивается, но анализ вариантов КИМ ЕГЭ профильного уровня и практика показывают, что в настоящее время этого достаточно для успешного решения задачи № 18 на экзамене.

В заключение отметим, что выстроить подобный курс самостоятельно, без преподавателя, обычный школьник не сможет, даже имея под рукой хорошие учебные пособия по методам решения задач с параметром. Здесь необходима помощь опытного наставника, который сможет подобрать нужные задачи и выстроить траекторию движения школьника по ним.

Заметим, кстати, что весьма эффективным инструментом для изучения именно методов решения задач с параметром являются интерактивные тренажеры с пошаговым разбором решения.

Работая с таким тренажером, школьник одновременно учится выстраивать логику решения задачи с параметром и контролирует правильность выполнения каждого шага решения. Это очень важное умение, так как одна из основных сложностей в решении задачи с параметром состоит в том, что необходимо на каждом шаге решения понимать, что означают уже полученные результаты и что (в зависимости от этих результатов) еще остается сделать, чтобы довести решение до конца.

Регулярно тренируйтесь в решении задач

Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:

• Начать заниматься бесплатно.
• Купить доступ к этой задаче в составе экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.

Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.

Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.

Что такое параметр? Простые задачи с параметрами

Одна из сложных задач Профильного ЕГЭ по математике — задача с параметрами. В ЕГЭ 2020 года это №18. И даже в вариантах ОГЭ они есть. Что же означает это слово — параметр?

Толковый словарь (в который полезно время от времени заглядывать) дает ответ: «Параметр — это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса».

Хорошо, параметр — это какая-либо характеристика, свойство системы или процесса.

Вот, например, ракета выводит космический аппарат в околоземное пространство. Как вы думаете — какие параметры влияют на его полет?

Если корабль запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту.

Вторая космическая скорость, приближенно равная 11,2 км/с, позволяет космическому кораблю преодолеть поле тяжести Земли. Третья космическая скорость, приближенно равная 16,7 км/с, дает возможность преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.

А если скорость меньше первой космической? Значит, тонны металла, топлива и дорогостоящей аппаратуры рухнут на землю, сопровождаемые репликой растерянного комментатора: «Кажется, что-то пошло не так».

Скорость космического корабля можно — параметр, от которого зависит его дальнейшая траектория и судьба. Конечно, это не единственный параметр. В реальных задачах науки и техники, задействованы уравнения, включающие функции многих переменных и параметров, а также производные этих функций.

1. Теперь пример из школьной математики.

Все мы помним, что такое квадратное уравнение. Это уравнение вида , где коэффициент а не равен нулю.

Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.

Дискриминант квадратного уравнения:

Если , квадратное уравнение имеет два корня: и

Если , квадратное уравнение имеет единственный корень

Если , квадратное уравнение не имеет действительных корней. Рассмотрим уравнение . Его дискриминант равен Если , то есть , это квадратное уравнение имеет два корня.

Если при , уравнение имеет единственный корень.

Если , то есть с > 1, корней нет.

В нашем уравнении с — параметр, величина, которая принимать любые значения. Но от этого параметра с зависит количество корней данного уравнения.

Для того чтобы уверенно решать задачи с параметрами, необходимо отличное знание и алгебры, и планиметрии.

И еще две простые задачи с параметром.

2. Найдите значение параметра p, при котором уравнение имеет 2 различных корня.

Квадратное уравнение имеет два различных корня, когда .

Найдем дискриминант уравнения

Т.к. , получим:

Вспомним, как решаются квадратичные неравенства (вы проходили это в 9 классе).

Найдем корни квадратного уравнения . Это и

Разложим левую часть неравенства на множители:

Рисуем параболу с ветвями вверх. Она пересекает ось р в точках и

3. При каких значениях параметра k система уравнений не имеет решений?

Оба уравнения системы — линейные. График линейного уравнения — прямая. Запишем уравнения системы в привычном для нас виде, выразив у через х:

Первое уравнение задает прямую с угловым коэффициентом . Второе уравнение — прямую с угловым коэффициентом -2.

Система уравнений не имеет решений, если эти прямые не пересекаются, то есть параллельны. Это значит, что и .

Действительно, в этом случае первое уравнение задает прямую , а второе — параллельную ей прямую

Урок по теме «Методы решения задач с параметрами»

Разделы: Математика

Цель данной работы – изучение различных способов решения задач с параметрами. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность. Для развития этих навыков необходимы длительнее усилия, именно поэтому в профильных 10-11 классах с углубленным изучением точных наук введен курс: “Математический практикум”, частью которого является решение уравнений и неравенств с параметрами. Курс входит в число дисциплин, включенных в компонент учебного плана школы.

Успешному изучению методов решения задач с параметрами могут помочь элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с параметрами”.

Рассмотрим четыре больших класса задач с параметрами:

1. Уравнения, неравенства и их системы, которые необходимо решить для любого значения параметра, либо для значений параметра, принадлежащих определенному множеству.
2. Уравнения, неравенства и их системы, для которых требуется определить количество решений в зависимости от значения параметра.
3. Уравнения, неравенства и их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения (системы, неравенства) имеют заданное число решений.
4. Уравнения, неравенства и их системы, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Методы решений задач с параметрами.

1. Аналитический метод.

Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.

Пример 1. Найдите все значения параметра a, при которых уравнение:

(2a – 1)x 2 + ax + (2a – 3) =0 имеет не более одного корня.

При 2a – 1 = 0 данное уравнение квадратным не является, поэтому случай a =1/2 разбираем отдельно.

Если a = 1/2, то уравнение принимает вид 1/2x – 2 = 0, оно имеет один корень.

Если a ≠ 1/2 , то уравнение является квадратным; чтобы оно имело не более одного корня необходимо и достаточно, чтобы дискриминант был неположителен:

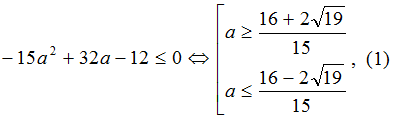
Чтобы записать окончательный ответ, необходимо понять,

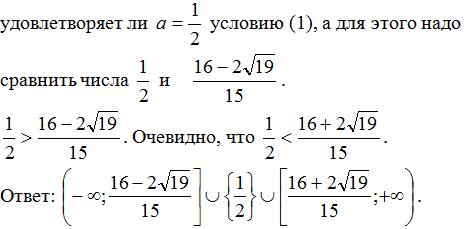
2. Графический метод.

В зависимости от задачи (с переменной x и параметром a) рассматриваются графики в координатной плоскости (x;y) или в плоскости (x;a).

Пример 2. Для каждого значения параметра a определите количество решений уравнения .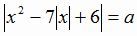

Заметим, что количество решений уравнения 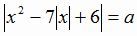равно количеству точек пересечения графиков функций 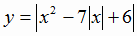и y = a.

График функции 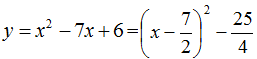показан на рис.1.

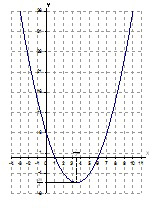
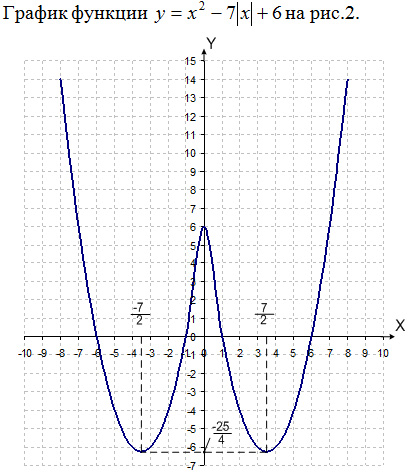
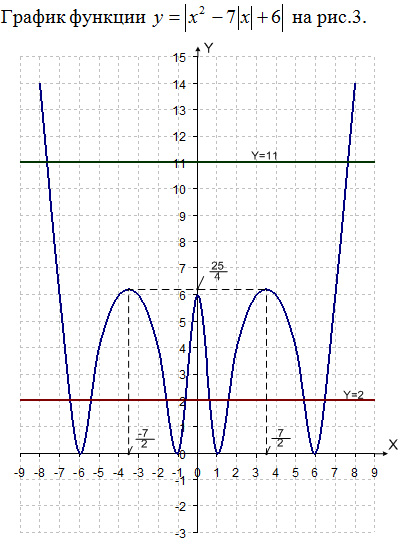
y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).

Ответ: при a 25/4 – два решения.

3. Метод решения относительно параметра.

При решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.

Пример 3. Найти все значения параметра а , при каждом из которых уравнение 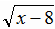= —ax +3a +2 имеет единственное решение.

Будем решать это уравнение заменой переменных. Пусть 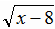= t , t ≥ 0 , тогда x = t 2 + 8 и уравнение примет вид at 2 + t + 5a – 2 = 0 . Теперь задача состоит в том, чтобы найти все а, при которых уравнение at 2 + t + 5a – 2 = 0 имеет единственное неотрицательное решение. Это имеет место в следующих случаях.

1) Если а = 0, то уравнение имеет единственное решение t = 2.

Решение некоторых типов уравнений и неравенств с параметрами.

Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности.

Решение каждой задачи своеобразно и требует к себе индивидуального, нестандартного подхода, поскольку не существует единого способа решения таких задач.

Задача № 1. При каких значениях параметра b уравнение 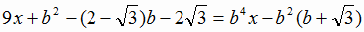не имеет корней?

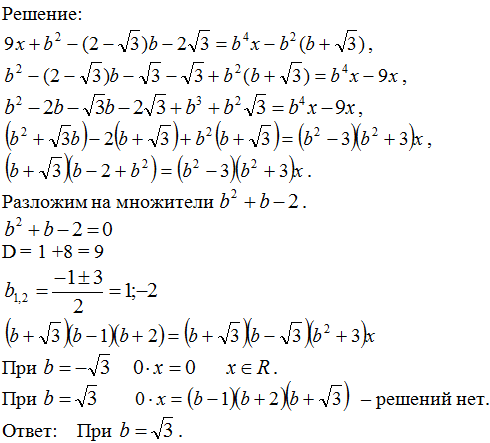
Ⅱ . Степенные уравнения, неравенства и их системы.

Задача №2. Найти все значения параметра a, при которых множество решений неравенства:

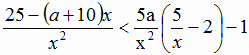содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.

.

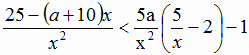Преобразуем обе части неравенства.

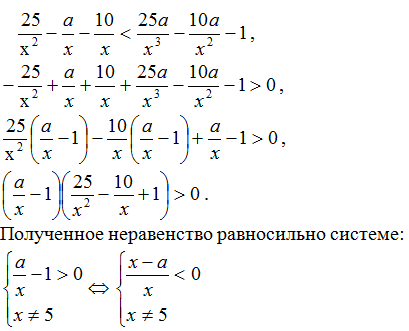
Для того, чтобы множество решений неравенства содержало число 6, необходимо и достаточно выполнение условия: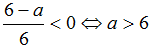

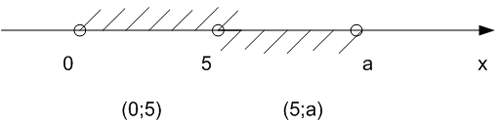Рис.4

При a > 6 множество решений неравенства: .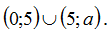

Интервал (0;5) не может содержать ни одного отрезка длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в интервале (5; a).

Это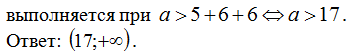

Ⅲ . Показательные уравнения, неравенства и системы.

Задача № 3. В области определения функции 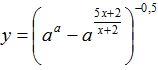взяли все целые положительные числа и сложили их. Найти все значения, при которых такая сумма будет больше 5, но меньше 10.

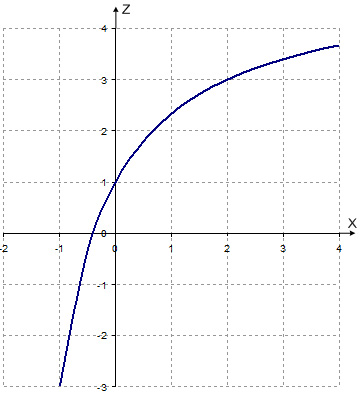
1) Графиком дробно-линейной функции 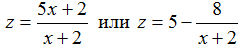является гипербола. По условию x > 0. При неограниченном возрастании х дробь 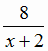монотонно убывает и приближается к нулю, а значения функции z возрастают и приближаются к 5. Кроме того, z(0) = 1.

2) По определению степени область определения D(y) состоит из решений неравенства 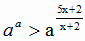. При a = 1 получаем неравенство, у которого решений нет. Поэтому функция у нигде не определена.

3) При 0 0 , то z(x) > z(0) = 1 . Значит, каждое положительное значение х является решением неравенства 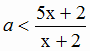. Поэтому для таких а указанную в условии сумму нельзя найти.

4) При a > 1 показательная функция с основанием а возрастает и неравенство 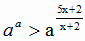равносильно неравенству 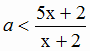. Если a ≥ 5 , то любое положительное число является его решением, и указанную в условии сумму нельзя найти. Если 1 7.05.2013

Как подготовиться к решению задач с параметром на ЕГЭ | 1С:Репетитор

Советы ведущего преподавателя курса 1С:Репетитор
Татьяны Александровны Чернецкой

Задание № 18 варианта КИМ ЕГЭ по математике профильного уровня

Задача с параметром – для обычного школьника одна из самых сложных задач варианта КИМ ЕГЭ: в программах по математике для общеобразовательных школ (за исключением профильных и специализированных классов, школ и лицеев) таким задачам либо не уделяется должного внимания, либо они не рассматриваются вовсе. Несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволяют продвинуться в решении задачи с параметром достаточно далеко и если уж не решить ее полностью, то хотя бы получить за нее некоторое количество баллов на экзамене.

Ранее, до появления единого государственного экзамена, задачи с параметрами входили в варианты вступительных экзаменов по математике в ведущие вузы, а сегодня входят в вариант КИМ ЕГЭ профильного уровня. Дело в том, что эти задачи обладают высокой диагностической ценностью: они позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности, а главное – насколько успешно он сможет овладеть курсом математики в вузе.

«Научите меня решать задачи с параметром», – такую просьбу я часто слышу от своих учеников. Что ж, эта задача потребует от выпускника немало интеллектуальных усилий. С чего начать изучение? С освоения методов решения задач с параметром. Собственно, если вы внимательно читали наши рекомендации, как подготовиться к решению сложных задач варианта КИМ ЕГЭ, то заметили, что это универсальный совет. Именно так построен наш курс «1С:Репетитор»: изучаем как можно более широкий спектр методов и приемов решения задач и тренируемся в применении этих методов на практике.

Чему нужно научиться, решая задачи с параметром

В первую очередь – правильно применять равносильные преобразования уравнений, неравенств и их систем. То есть понять, при каких ограничениях, накладываемых на параметр, можно выполнять то или иное преобразование. Лучше всего начать с заданий вида: «Для каждого значения параметра решить…» и рассмотреть по возможности все основные элементарные функции, встречающиеся в школьном курсе математики.

Если с несложными задачами такого вида школьник справляется неплохо, то можно переходить к изучению аналитических методов решения задач, содержательно усложняя и классифицируя задачи с точки зрения применения к ним этих методов исследования. Имеется в виду знакомство с подходами к решению задач, содержащих формулировки типа: «При каких значениях параметра уравнение (неравенство, система) имеет одно (два, три, бесконечно много и т.д.) решений», «При каких значениях параметра решением уравнения (неравенства, системы) является некоторое подмножество множества действительных чисел» и т.д.

Следующий шаг, который мы рекомендуем, – тщательно изучить схему исследования квадратичной функции. Поскольку квадратичная функция является одной из самых хорошо изученных в школьном курсе математики, на ее основе можно предложить большое количество исследовательских задач, разнообразных по форме и содержанию, чем и пользуются составители вариантов КИМ ЕГЭ.

Мы рекомендуем подойти к рассмотрению данных задач по следующей схеме: