Как определить интервалы возрастания и убывания функции

Возрастание и убывание функций

1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

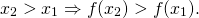x_1 Rightarrow f(x_2 ) > f(x_1 ). ]» title=»Rendered by QuickLaTeX.com»/>

2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

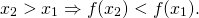x_1 Rightarrow f(x_2 )

Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.

График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).

На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).

Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x₁;x₅]:

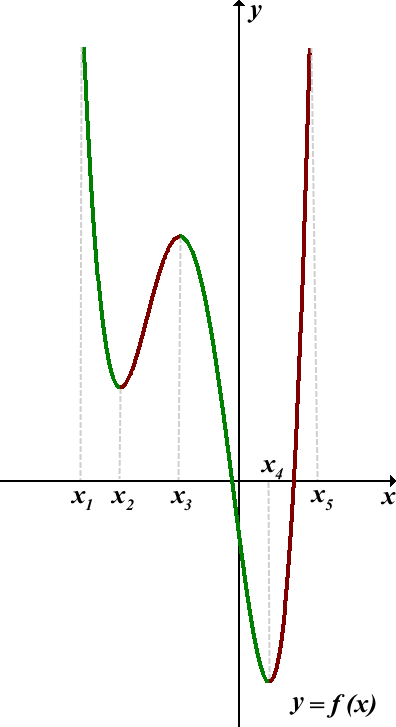
Кратко это записывают так:

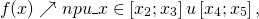
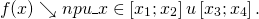
3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).

4) Если функция возрастает на всей своей области определения, то её называют возрастающей.

Если функция убывает на всей своей области определения, то её называют убывающей.

Например, y=√x, y=x³ — возрастающие функции.

Линейная функция y=kx+b возрастающая при k>0 и убывающая при k

то функция y=f(x) называется неубывающей на этом промежутке.

6) Если для любых двух значений x₁,x₂ из некоторого промежутка выполняется условие

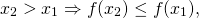x_1 Rightarrow f(x_2 ) le f(x_1 ), ]» title=»Rendered by QuickLaTeX.com»/>

то функция y=f(x) называется невозрастающей на этом промежутке.

7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.

Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x₁;x₃], является невозрастающей и неубывающей:

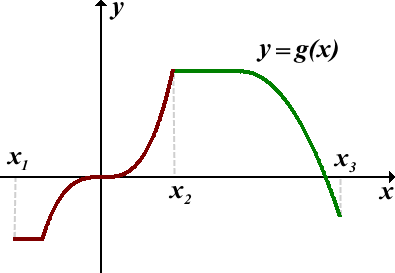
Функция y=g(x) является неубывающей на промежутке [x₁;x₂].

Функция y=g(x) является невозрастающей на промежутке [x₂;x₃].

Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.

Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?

группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:

Теперь выносим общий множитель (x₂-x₁) за скобки:

Так как x₂>x₁, то x₂-x₁>0. Следовательно, знак произведения зависит от знака второго множителя.

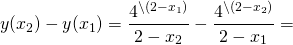
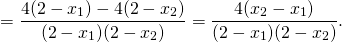
0. ]» title=»Rendered by QuickLaTeX.com»/>

Отсюда y(x₂)-y(x₁)>0. Поэтому данная функция возрастает на промежутке (2;+∞).

Что и требовалось доказать.

Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).

Алгебра и начала математического анализа. 11 класс

Возрастание и убывание функции

Каждой функции поставьте в соответствие её промежутки монотонности.

Возрастание и убывание функции

Посмотрите на рисунок. Укажите число промежутков убывания функции [у=f(x),] график которой изображен на рисунке.

1. 5
2. 4
3. 9

Возрастание и убывание функции

Найдите промежутки возрастания и убывания функции [у= 2х^2 — 8х+10]

Возрастание и убывание функции

Найдите по графикам количество промежутков возрастания функции и впишите ответ:

Возрастание и убывание функции

Заполните пропуски в тексте:

Функция $y=f(x)$ на X, если для любых $x_1 и x_2$ , $x_1gt x_2$ из этого промежутка выполняется неравенство $f(x_1)gt f(x_2)$. Другими словами – значению аргумента соответствует большее значение

Возрастание и убывание функции

Возрастание и убывание функции

Соедините последовательно точки так, чтобы график функции сначала убывал, затем возрастал и снова убывал.

Загрузите и распечатайте документ для выполнения задания

Возрастание и убывание функции

Подчеркните верный ответ.

На рисунке изображён график $y=f'(x)$ — производной функции $f(x),$ определенной на интервале $(-8; 3)$. На каком интервале функция $f(x)$ возрастает?

1. $(-8; -3]$;
2. $[3; 8)$;
3. $(-∞; +∞)$.

Возрастание и убывание функции

На рисунке изображен график производной функции $f(x)$, определенной на интервале $(-2; 9)$. Ответьте на вопросы по данному графику.

1. Каково количество промежутков возрастания функции $f(x)$?

2. Какова сумма целых точек, входящих в промежутки возрастания?

3. Какова сумма целых точек, входящих в промежутки убывания?

4. Какова длина промежутка возрастания функции на интервале $(-2;8]$?

Возрастание и убывание функции

На рисунке изображен график производной функции $f(x)$, определенной на интервале $(-9; 8)$. Найдите промежутки возрастания функции $f(x)$. В ответе укажите длину наибольшего из них.

1. 7;
2. 8;
3. 6.

Возрастание и убывание функции

На рисунке изображен график производной функции $f(x)$, определенной на интервале $(-6; 7)$. Найдите промежутки возрастания функции $f(x)$. В ответе укажите сумму целых точек, входящих в эти промежутки.