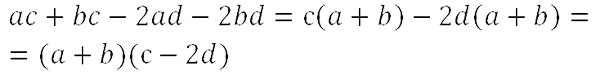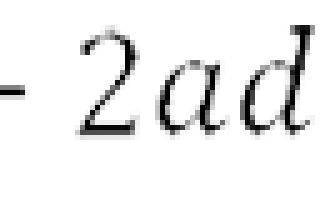Получим способ разложения xy
Разложение многочлена на множители
Содержание:
Для того, чтобы разложить на множители, необходимо упрощать выражения. Это необходимо для того, чтобы можно было в дальнейшем сократить. Разложение многочлена имеет смысл тогда, когда его степень не ниже второй. Многочлен с первой степенью называют линейным.
Статья раскроет все понятия разложения, теоретические основы и способы разложений многочлена на множители.
Теория
Когда любой многочлен со степенью n , имеющие вид P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 , представляют в виде произведения с постоянным множителем со старшей степенью a n и n линейных множителей ( x — x i ) , i = 1 , 2 , … , n , тогда P n ( x ) = a n ( x — x n ) ( x — x n — 1 ) · . . . · ( x — x 1 ) , где x i , i = 1 , 2 , … , n – это и есть корни многочлена.
Теорема предназначена для корней комплексного типа x i , i = 1 , 2 , … , n и для комплексных коэффициентов a k , k = 0 , 1 , 2 , … , n . Это и есть основа любого разложения.
Когда коэффициенты вида a k , k = 0 , 1 , 2 , … , n являются действительными числами, тогда комплексные корни, которые будут встречаться сопряженными парами. Например, корни x 1 и x 2 , относящиеся к многочлену вида P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 считаются комплексно сопряженным, тогда другие корни являются действительными, отсюда получаем, что многочлен примет вид P n ( x ) = a n ( x — x n ) ( x — x n — 1 ) · . . . · ( x — x 3 ) x 2 + p x + q , где x 2 + p x + q = ( x — x 1 ) ( x — x 2 ) .
Замечание
Корни многочлена могут повторяться. Рассмотрим доказательство теоремы алгебры, следствия из теоремы Безу.
Основная теорема алгебры
Любой многочлен со степенью n имеет как минимум один корень.
Теорема Безу
После того, как произвели деление многочлена вида P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 на ( x — s ) , тогда получаем остаток, который равен многочлену в точке s , тогда получим
P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = ( x — s ) · Q n — 1 ( x ) + P n ( s ) , где Q n — 1 ( x ) является многочленом со степенью n — 1 .
Следствие из теоремы Безу
Когда корень многочлена P n ( x ) считается s , тогда P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = ( x — s ) · Q n — 1 ( x ) . Данное следствие является достаточным при употреблении для описания решения.
Разложение на множители квадратного трехчлена
Квадратный трехчлен вида a x 2 + b x + c можно разложить на линейные множители. тогда получим, что a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 ) , где x 1 и x 2 — это корни (комплексные или действительные).
Отсюда видно, что само разложение сводится к решению квадратного уравнения впоследствии.
Произвести разложение квадратного трехчлена на множители.
Необходимо найти корни уравнения 4 x 2 — 5 x + 1 = 0 . Для этого необходимо найти значение дискриминанта по формуле, тогда получим D = ( — 5 ) 2 — 4 · 4 · 1 = 9 . Отсюда имеем, что
x 1 = 5 — 9 2 · 4 = 1 4 x 2 = 5 + 9 2 · 4 = 1
Отсюда получаем, что 4 x 2 — 5 x + 1 = 4 x — 1 4 x — 1 .
Для выполнения проверки нужно раскрыть скобки. Тогда получим выражение вида:
4 x — 1 4 x — 1 = 4 x 2 — x — 1 4 x + 1 4 = 4 x 2 — 5 x + 1
После проверки приходим к исходному выражению. То есть можно сделать вывод, что разложение выполнено верно.
Произвести разложение на множители квадратный трехчлен вида 3 x 2 — 7 x — 11 .
Получим, что необходимо вычислить получившееся квадратное уравнение вида 3 x 2 — 7 x — 11 = 0 .
Чтобы найти корни, надо определить значение дискриминанта. Получим, что
3 x 2 — 7 x — 11 = 0 D = ( — 7 ) 2 — 4 · 3 · ( — 11 ) = 181 x 1 = 7 + D 2 · 3 = 7 + 181 6 x 2 = 7 — D 2 · 3 = 7 — 181 6
Отсюда получаем, что 3 x 2 — 7 x — 11 = 3 x — 7 + 181 6 x — 7 — 181 6 .
Произвести разложение многочлена 2 x 2 + 1 на множители.
Теперь нужно решить квадратное уравнение 2 x 2 + 1 = 0 и найти его корни. Получим, что
2 x 2 + 1 = 0 x 2 = — 1 2 x 1 = — 1 2 = 1 2 · i x 2 = — 1 2 = — 1 2 · i
Эти корни называют комплексно сопряженными, значит само разложение можно изобразить как 2 x 2 + 1 = 2 x — 1 2 · i x + 1 2 · i .
Произвести разложение квадратного трехчлена x 2 + 1 3 x + 1 .
Для начала необходимо решить квадратное уравнение вида x 2 + 1 3 x + 1 = 0 и найти его корни.
x 2 + 1 3 x + 1 = 0 D = 1 3 2 — 4 · 1 · 1 = — 35 9 x 1 = — 1 3 + D 2 · 1 = — 1 3 + 35 3 · i 2 = — 1 + 35 · i 6 = — 1 6 + 35 6 · i x 2 = — 1 3 — D 2 · 1 = — 1 3 — 35 3 · i 2 = — 1 — 35 · i 6 = — 1 6 — 35 6 · i
Получив корни, запишем
x 2 + 1 3 x + 1 = x — — 1 6 + 35 6 · i x — — 1 6 — 35 6 · i = = x + 1 6 — 35 6 · i x + 1 6 + 35 6 · i
Если значение дискриминанта отрицательное, то многочлены останутся многочленами второго порядка. Отсюда следует, что раскладывать их не будем на линейные множители.
Способы разложения на множители многочлена степени выше второй
При разложении предполагается универсальный метод. Большинство всех случаев основано на следствии из теоремы Безу. Для этого необходимо подбирать значение корня x 1 и понизить его степень при помощи деления на многочлена на 1 делением на ( x — x 1 ) . Полученный многочлен нуждается в нахождении корня x 2 , причем процесс поиска цикличен до тех пор, пока не получим полное разложение.
Если корень не нашли, тогда применяются другие способы разложения на множители: группировка, дополнительные слагаемые. Данная тема полагает решение уравнений с высшими степенями и целыми коэффициентами.
Вынесение общего множителя за скобки
Рассмотрим случай, когда свободный член равняется нулю, тогда вид многочлена становится как P n ( x ) = a n x n + a n — 1 x n — 1 + . . . + a 1 x .
Видно, что корень такого многочлена будет равняться x 1 = 0 , тогда можно представить многочлен в виде выражения P n ( x ) = a n x n + a n — 1 x n — 1 + . . . + a 1 x = = x ( a n x n — 1 + a n — 1 x n — 2 + . . . + a 1 )
Данный способ считается вынесением общего множителя за скобки.
Выполнить разложение многочлена третьей степени 4 x 3 + 8 x 2 — x на множители.
Видим, что x 1 = 0 — это корень заданного многочлена, тогда можно произвести вынесение х за скобки всего выражения. Получаем:
4 x 3 + 8 x 2 — x = x ( 4 x 2 + 8 x — 1 )
Переходим к нахождению корней квадратного трехчлена 4 x 2 + 8 x — 1 . Найдем дискриминант и корни:
D = 8 2 — 4 · 4 · ( — 1 ) = 80 x 1 = — 8 + D 2 · 4 = — 1 + 5 2 x 2 = — 8 — D 2 · 4 = — 1 — 5 2
Тогда следует, что
4 x 3 + 8 x 2 — x = x 4 x 2 + 8 x — 1 = = 4 x x — — 1 + 5 2 x — — 1 — 5 2 = = 4 x x + 1 — 5 2 x + 1 + 5 2
Разложение на множители многочлена с рациональными корнями
Для начала примем за рассмотрение способ разложения, содержащий целые коэффициенты вида P n ( x ) = x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 , где коэффициента при старшей степени равняется 1 .
Когда многочлен имеет целые корни, тогда их считают делителями свободного члена.
Способ группировки
Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.
Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.
Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.
- Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
- Вынести общий множитель за скобки у каждой группы одночленов.
- Вынести полученный общий многочлен за скобки.
Рассмотрим пример разложения многочлена на множители способом группировки.
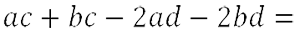
- Подчеркнем повторяющиеся буквенные множители в одночленах.
 У нас получится две группы одночленов с повторяющимися буквенными множителями.
У нас получится две группы одночленов с повторяющимися буквенными множителями. 
- Вынесем общий множитель за скобки у каждой группы одночленов.
 П роверим, верно ли мы вынесли общий множитель за скобки. Для этого раскроем скобки обратно.
П роверим, верно ли мы вынесли общий множитель за скобки. Для этого раскроем скобки обратно.  М ы получили исходный многочлен, значит, мы правильно вынесли общий множитель за скобки.
М ы получили исходный многочлен, значит, мы правильно вынесли общий множитель за скобки. - Теперь в полученном результате вынесем общий многочлен « (a + b) » за скобки.

Примеры способа группировки
Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен .
Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.
Первый способ
Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.
48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )
Второй способ
Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.
48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)
В итоге получился такой же ответ, как и при первом способе.
Рассмотрим еще один пример разложения многочлена способом группировки.
- 4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1) = (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1) , что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.
Смена знаков в скобках
Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.
Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.
2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)
Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.
- 2m(m − n) + n − m = − 2m( − m + n) + (n − m) = −2m(n − m) + 1 · (n − m) =
= (n − m)(−2m + 1)
Получим способ разложения xy
Ключевые слова: множители, разложение на множители, вынесение общего множителя, формулы сокращенного умножения, способ группировки, метод выделения полного квадрата.
Тождественное преобразование, приводящее к произведению нескольких множителей — многочленов или одночленов, называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.
- Вынесение общего множителя за скобки. Это преобразование является непосредственным следствием распределительного закона ac + bc = c(a + b)
- Пример. Разложить многочлен на множители 12 y 3 – 20 y 2 . Решение. Имеем: 12 y 3 – 20 y 2 = 4 y 2 · 3 y – 4 y 2 · 5 = 4 y 2 (3 y – 5). Ответ. 4 y 2 (3 y – 5).
- Использование формул сокращенного умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.
- Пример. Разложить на множители многочлен x 4 – 1. Решение. Имеем: x 4 – 1 = ( x 2 ) 2 – 1 2 = ( x 2 – 1)( x 2 + 1) = ( x 2 – 1 2 )( x 2 + 1) = ( x + 1)( x – 1)( x 2 + 1). Ответ. ( x + 1)( x – 1)( x 2 + 1).
- Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.
- Пример. Разложить на множители многочлен x 3 – 3 x 2 y – 4 xy + 12 y 2 . Решение. Сгруппируем слагаемые следующим образом:
x 3 – 3 x 2 y – 4 xy + 12 y 2 = ( x 3 – 3 x 2 y ) – (4 xy – 12 y 2 ). В первой группе вынесем за скобку общий множитель x 2 , а во второй − 4 y . Получаем:
( x 3 – 3 x 2 y ) – (4 xy – 12 y 2 ) = x 2 ( x – 3 y ) – 4 y ( x – 3 y ). Теперь общий множитель ( x – 3 y ) также можно вынести за скобки:
x 2 ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x 2 – 4 y ). Ответ. ( x – 3 y )( x 2 – 4 y ).
- Способ выделения полного квадрата. Метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов.
- Пример. Разложить на множители многочлен x 4 + 4 x 2 – 1. Решение. Имеем $$x^ <4>+4x^<2>— 1 = x^ <4>+2 cdot 2x^ <2>+ 4 — 4 — 1 = (x^ <2>+ 2)^ <2>— 5 = (x^ <2>+ 2 -sqrt<5>)(x^ <2>+ 2 -sqrt<5>)$$.
- Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
- Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
- Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.
Пример. Разложить на множители многочлен 3 x 3 – x 2 – 3 x + 1.
Решение. Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax 2 + bx + c такие, что справедливо равенство 3 x 3 – x 2 – 3 x + 1 = ( x – p )( ax 2 + bx + c ) = ax 3 + ( b – ap ) x 2 + ( c – bp ) x – pc . Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырех уравнений для определения четырех неизвестных коэффициентов:
Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители: 3 x 3 – x 2 – 3 x + 1 = ( x – 1)(3 x 2 + 2 x – 1).
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №13. Многочлены от нескольких переменных.
Перечень вопросов, рассматриваемых в теме
1) определение многочлена от нескольких переменных;
2) понятие симметрических многочленов;
3) формулы сокращенного умножения для старших степеней;
4) бином Ньютона;
5) метод неопределенных коэффициентов.
Глоссарий по теме
Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.
Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х.
Уравнение Р(x;y) = а, где  , называютсимметрическим, если Р(х;y) — симметрический многочлен.
, называютсимметрическим, если Р(х;y) — симметрический многочлен.
Треугольник Паскаля —бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Многочлены от нескольких переменных можно складывать, вычитать, перемножать, возводить в натуральную степень, разлагать на множители — это вам известно из курса алгебры 7—9-го классов. Этот урок позволит нам несколько расширить знания о многочленах.
Пример 1. Разложить на множители многочлен: 2x 2 -5xy+2y 2 .
Воспользуемся методом группировки
2x 2 -5xy+2y 2= 2x 2 -4xy-xy+2y 2 = 2x(x-2y) –y(x-2y)=
Пример 2. Выведем формулу сокращенного умножения для «квадрата суммы» (x+y+z+u) 2 .
(x+y+z+u) 2 =((x+y)+(z+u)) 2 = (x+y) 2 +2(x+y)(z+u)+(z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).
Итак, мы получили (x+y+z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).
Среди многочленов от двух переменных выделяют однородные и симметрические многочлены.
Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.
1) р(х; у)=2х+3у – однородный многочлен первой степени; соответственно 2х+3у=0 – однородное уравнение первой степени.
2) р(х; у)=3х 2 +5ху-7у 2 — однородный многочлен второй степени; соответственно 3х 2 +5ху-7у 2 =0 — однородное уравнение второй степени.
3) p(x; y)= x 3 +4xy 2 -5y 3 — однородный многочлен третьей степени; x 3 +4xy 2 -5y 3 =0 соответственно — однородное уравнение третьей степени.
4) p(x; y)= anx n +an-1x n-1 y+an-2x n-2 y 2 +…+a1xy n-1 +ay n — общий вид однородного многочлена n-й степени.
Рассмотрим еще один метод разложения многочленов на множители-
метод неопределенных коэффициентов. Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения
- Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
- Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
- Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.
Пример 3. Разложить на множители многочлен
3 x 3 – x 2 – 3 x + 1.
Решение. Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax 2 + bx + c такие, что справедливо равенство 3 x 3 – x 2 – 3 x + 1 = ( x – p )( ax 2 + bx + c ) = ax 3 + ( b – ap ) x 2 + ( c – bp ) x – pc . Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырех уравнений для определения четырех неизвестных коэффициентов:

Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители: 3 x 3 – x 2 – 3 x + 1 = ( x – 1)(3 x 2 + 2 x – 1).
Стоит отметить, что существует достаточно изящный способ решения однородных уравнений. Поясним его суть на примере.
Пример 4. Решим уравнение x 3 +4xy 2 -5y 3 =0
Заметим, что если в заданном уравнении взять х=0, то получится у=0; это означает, что пара (0; 0) является решением однородного уравнения. Пусть теперь х . Разделим почленно обе части заданного однородного уравнения на х 3 , получим:
. Разделим почленно обе части заданного однородного уравнения на х 3 , получим:

Введем новую переменную  . Тогда уравнение примет вид 1+4z 2 -5z 3 =0.
. Тогда уравнение примет вид 1+4z 2 -5z 3 =0.
Далее последовательно находим:
(5z 3 -5z 2 )+(z 2 -1)=0
Из уравнения z-1=0 находим z=1, уравнение 5z 3 -4z 2 -1=0 действительных корней не имеет.
Если z=1, то  , т.е. у=х. Это значит, что любая пара вида (t; t) является решением заданного однородного уравнения. Между прочим, и отмеченная нами ранее пара (0; 0) также входит в указанный перечень решений.
, т.е. у=х. Это значит, что любая пара вида (t; t) является решением заданного однородного уравнения. Между прочим, и отмеченная нами ранее пара (0; 0) также входит в указанный перечень решений.
Ответ: (t; t), где t- любое действительное число.
Теперь поговорим о симметрических многочленах. Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х. Например, симметрическим является двучлен x 2 y+xy 2 . В самом деле, при одновременной замене х на у и у на х получится двучлен y 2 x+yx 2 , но это то же самое, что x 2 y+xy 2 . Другие примеры симметрических многочленов: xy, x+y, x 2 +y 2 , x 3 +y 3 , x 4 +y 4 и т.д. Первые два из записанных многочленов считаются основными в том смысле, что любые другие симметрические многочлены можно представить в виде некоторой комбинации многочленов х + у и ху.
Теорема. Любой симметрический многочлен Р(х;у) можно представить в виде многочлена от ху и х+у.
x 2 +y 2 =(x+y) 2 -2xy
x 3 +y 3 =(x+y) 3 -3xy(x+y)
x 4 +y 4 = 2xy(x 2 +y 2 )-(x 4 +y 4 )+3(xy) 2 и т.д.
Уравнение Р(x;y) = а, где  , называют симметрическим, если Р(х;y) — симметрический многочлен. Мы с вами рассматривали его на предыдущем уроке.
, называют симметрическим, если Р(х;y) — симметрический многочлен. Мы с вами рассматривали его на предыдущем уроке.
А теперь перейдем к такому понятию как бином Ньютона.
Слово бином означает «Два числа». В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Бином Ньютона — название формулы, выражающей степень двучлена в виде суммы одночленов.
Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.
Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.
(a+b) 2 =a 2 +2ab+b 2
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3
Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах
Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?
Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):
(a+b) 4 =(a+b) 3 (a+b)=(a 3 +3a 2 b+3ab 2 +b 3 )(a+b)=a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4
(a+b) 5 =(a+b) 4 (a+b)=(a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4 )(a+b)=a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +b 5
Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:
Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):
Общая формула бинома Ньютона:
 .
.
Правая часть формулы называется разложением степени бинома.
 — называется биномиальными коэффициентами, а все слагаемые — членами бинома.
— называется биномиальными коэффициентами, а все слагаемые — членами бинома.
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.
На самом деле, о треугольнике Паскаля было известно задолго до Паскаля — его знал живший в XI-XII вв. среднеазиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло). Первое, дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел  (биномиальных коэффициентов) до n=12 включительно.
(биномиальных коэффициентов) до n=12 включительно.
Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.
В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Доказать, что значение выражения 5 n +28n-1, где n – натуральное число, делится на 16 без остатка.
Решение: представим первое слагаемое выражение как 5 n = (4+1) n и воспользуемся формулой бинома Ньютона:

Полученное произведение доказывает делимость исходного выражения на 16.
Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница
Примеры и разборы решения заданий тренировочного модуля
Из данных многочленов выделите симметрические:
- 2х 2 -5ху+2у 2 -6
- 6x⁴-16xy²-6y 3 +19
- -3ху+6х²-5у²+8
- 16x 4 y²+16x²y 4 -x⁴-y⁴
Решение: к данному заданию применим определение симметрических многочленов (Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х). Получим, что нам подходят 1 и 4 пункты.
- 2х 2 -5ху+2у 2 -6
- 6x⁴-16xy²-6y 3 +19
- -3ху+6х²-5у²+8
- 16x 4 y²+16x²y 4 -x⁴-y⁴
(а+b) 5 = __a 5 +___a 4 b+___a 3 b 2 +___a 2 b 3 +___ab 4 +__b 5
Решение: для решения данного задания воспользуемся треугольником Паскаля
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Нас интересует последняя строчка.
Применив ее, получим ответ:
(а+b) 5 = 1a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +1b 5


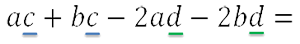 У нас получится две группы одночленов с повторяющимися буквенными множителями.
У нас получится две группы одночленов с повторяющимися буквенными множителями. 
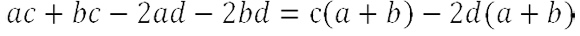 П роверим, верно ли мы вынесли общий множитель за скобки. Для этого раскроем скобки обратно.
П роверим, верно ли мы вынесли общий множитель за скобки. Для этого раскроем скобки обратно. 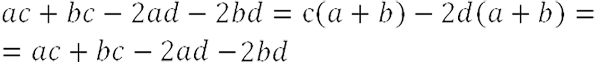 М ы получили исходный многочлен, значит, мы правильно вынесли общий множитель за скобки.
М ы получили исходный многочлен, значит, мы правильно вынесли общий множитель за скобки.