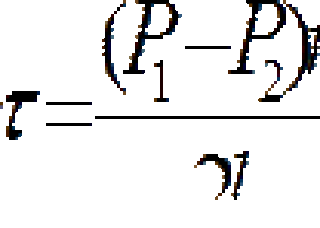Основы теория ламинарного течения жидкости
Ламинарный режим движения жидкости. Основы теория ламинарного течения жидкости
Фотография ламинарного течения
Ламинарный поток — спокойное течение жидкости или газа без перемешивания. Жидкость или газ перемещаются слоями, которые скользят друг относительно друга. По мере того, как увеличивается скорость движения слоев, или по мере уменьшения вязкости жидкости ламинарный поток превращается в турбулентный . Для каждой жидкости или газа эта точка наступает при определенной величине числа Рейнольдса .
Описание
Ламинарные течения наблюдаются или у очень вязких жидкостей , или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров. В частности, ламинарные течения имеют место в узких (капиллярных) трубках, в слое смазки в подшипниках, в тонком пограничном слое, который образуется вблизи поверхности тел при обтекании их жидкостью или газом, и др. С увеличением скорости движения данной жидкости ламинарное течение может в некоторый момент перейти в неупорядоченное турбулентное течение . При этом резко изменяется сила сопротивления движению. Режим течения жидкости характеризуется так называемым числом Рейнольдса (Re) .
Когда значение Re меньше некоторого критического числа Re kp , имеет место ламинарные течения жидкости; если Re > Re kp , режим течения может стать турбулентным . Значение Re кр зависит от вида рассматриваемого течения. Так, для течения в круглых трубах Rе кр ≈ 2200 (если характерной скоростью считать среднюю по сечению скорость, а характерным размером — диаметр трубы). Следовательно, при Re kp Δ, трубы считаются гидравлически гладкими. При δ Rekp, режим течения может стать турбулентным. Значение Рекр зависит от вида рассматриваемого течения. Так, для течения в круглых трубах Рекр » 2200 (если характерной скоростью считать среднюю по сечению скорость, а характерным размером ≈ диаметр трубы). Следовательно, при Rekp Reкр — турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re = 4000, а при Re = 2300 — 4000 имеет место переходная критическая область.
Смена режима течения при достижении Re кр обусловлена тем, что одно течение теряет устойчивость, а другое — приобретает.
Рассмотрим более подробно ламинарное течение.
Одним из наиболее простых видов движения вязкой жидкости является ламинарное движение в цилиндрической трубе, а в особенности его частный случай — установившееся равномерное движение. Теория ламинарного движения жидкости основывается на законе трения Ньютона . Это трение между слоями движущейся жидкости является единственным источником потерь энергии.
Рассмотрим установленное ламинарное течение жидкости в прямой трубе с d = 2 r 0
Чтобы исключить влияние силы тяжести и этим упростить вывод допустим, что труба расположена горизонтально.
Пусть в сечении 1-1 давление равно P 1 а в сечении 2-2 — P 2.
Ввиду постоянства диаметра трубы V = const, £ = const, тогда уравнение Бернулли для выбранных сечений примет вид:
Отсюда , что и будут показывать пьезометры, установленные в сечениях.
В потоке жидкости выделим цилиндрический объем.
Запишем уравнение равномерного движения выделенного объема жидкости, то есть равенство 0 суммы сил, действующих на объем.

Отсюда следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в зависимости от радиуса.
Если выразить касательное напряжение t по закону Ньютона, то будем иметь
Знак минус обусловлен тем, что направление отсчета r (от оси к стенке противоположного направления отсчета y (от стенки)
И подставить значение t в предыдущее уравнение, то получим

Отсюда найдем приращение скорости.

Выполнив интегрирование получим.

Постоянную интегрирования найдем из условия при r = r 0; V = 0
Скорость по окружности радиусом r равна

Это выражение является законом распределения скорости по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой второй степени. Максимальная скорость, имеющая место в центре сечения при r = 0 равна

Применим полученный закон распределения скоростей для расчета расхода.
Площадку dS целесообразно взять в виде кольца радиусом r и шириной dr
Тогда 
После интегрирования по всей площади поперечного сечения, то есть от r = 0, до r = r 0

Для получения закона сопротивления выразим; (через предыдущую формулу расхода)
 (
(
µ=υρ r 0 = d/2 γ = ρg. Тогда получим закон Пуарейля;
Основы теория ламинарного течения жидкости
Как показывают опыты, возможны два режима течения жидкостей и газов: ламинарный и турбулентный.
Ламинарным называется сложное течение без перемешивания частиц жидкости и без пульсаций скоростей и давлений. При ламинарном движении жидкости в прямой трубе постоянного поперечного сечения все линии тока направлены параллельно оси труб, отсутствуют поперечные перемещения жидкости. Однако, ламинарное движение нельзя считать безвихревым, так как в нем хотя и нет видимых вихрей, но одновременно с поступательным движением имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров с некоторыми угловыми скоростями.
Турбулентным называется течение, cопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При турбулентном течении наряду с основным продольным перемещением жидкости происходят поперечные перемещения и вращательное движение отдельных объемов жидкости.
Изменение режима течения происходит при определенном соотношении между скоростью V, диаметром d, и вязкостью υ. Эти три фактора входят в формулу безразмерного критерия Рейнольдса Re = Vd/υ, поэтому вполне закономерно, что именно число Re, является критерием, определяющим режим течения в трубах.
Число Re, при котором ламинарное движение приходит в турбулентное, называется критическим Reкр.
Как показывают опыты, для труб круглого сечения Rекр = 2300, то есть при Re Reкр – турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re = 4000, а при Re = 2300 – 4000 имеет место переходная критическая область.
Смена режима течения при достижении Re кр обусловлена тем, что одно течение теряет устойчивость, а другое – приобретает.
Рассмотрим более подробно ламинарное течение.
Одним из наиболее простых видов движения вязкой жидкости является ламинарное движение в цилиндрической трубе, а в особенности его частный случай — установившееся равномерное движение. Теория ламинарного движения жидкости основывается на законе трения Ньютона. Это трение между слоями движущейся жидкости является единственным источником потерь энергии.
Рассмотрим установленное ламинарное течение жидкости в прямой трубе с d = 2 r
Чтобы исключить влияние силы тяжести и этим упростить вывод допустим, что труба расположена горизонтально.
Пусть в сечении 1-1 давление равно P1 а в сечении 2-2 – P2.
Ввиду постоянства диаметра трубы V = const, £ = const, тогда уравнение Бернулли для выбранных сечений примет вид :
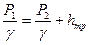 отсюда
отсюда 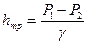 , что и будут показывать пьезометры, установленные в сечениях.
, что и будут показывать пьезометры, установленные в сечениях.
В потоке жидкости выделим цилиндрический объем.
Запишем уравнение равномерного движения выделенного объема жидкости, то есть равенство 0 суммы сил, действующих на объем.
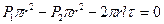
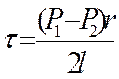
Отсюда следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в зависимости от радиуса.
Если выразить касательное напряжение t по закону Ньютона, то будем иметь
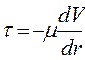
Знак минус обусловлен тем, что направление отсчета r ( от оси к стенке противоположного направления отсчета y ( от стенки)
И подставить значение t в предыдущее уравнение, то получим
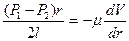
Отсюда найдем приращение скорости.
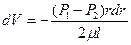
Выполнив интегрирование получим.
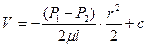
Постоянную интегрирования найдем из условия при r = r0; V = 0
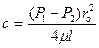
Скорость по окружности радиусом r равна
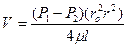
Это выражение является законом распределения скорости по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой второй степени. Максимальная скорость, имеющая место в центре сечения при r = 0 равна
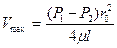
Применим полученный закон распределения скоростей для расчета расхода.
Площадку dS целесообразно взять в виде кольца радиусом r и шириной dr
Тогда 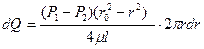
После интегрирования по всей площади поперечного сечения, то есть от r = 0, до r = r
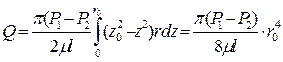
Для получения закона сопротивления выразим; (через предыдущую формулу расхода)
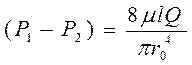 (
(
µ=υρ r = d/2 γ = ρg. Тогда получим закон Пуарейля ;
Ламинарное и турбулентное течение жидкости
Единицей измерения вязкости в СИ является 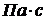 . Вязкость зависит от природы жидкости и температуры. Она может быть измерена с помощью специальных приборов, которые называются вискозиметрами. Часто ограничиваются определением относительной вязкости жидкости, которая равна отношению ее вязкости к вязкости воды.
. Вязкость зависит от природы жидкости и температуры. Она может быть измерена с помощью специальных приборов, которые называются вискозиметрами. Часто ограничиваются определением относительной вязкости жидкости, которая равна отношению ее вязкости к вязкости воды.
Ньютоновские и неньютоновские жидкости
Не для всех жидкостей можно описать силу трения с помощью уравнения Ньютона. Это уравнение применимо лишь к тем жидкостям, вязкость которых определяется только их природой и температурой и не зависит от скорости их течения. К этой категории относятся однородные низкомолекулярные жидкости (вода, спирт и т. д.) Жидкости такого рода называются ньютоновскими. Уравнение Ньютона неприменимо к жидкостям, неоднородным по своему составу. К ним относят суспензии, эмульсии, пены и также растворы веществ, состоящих из крупных молекул, имеющих форму длинных цепочек. Такие жидкости называются неньютоновскими.
Реологические свойства неньютоновских жидкостей зависят от деформируемости и прочности, входящих в них структурных элементов, от особенностей их движения, способности объединяться в агрегаты. Присутствие в жидкости взвешенных частиц или других включений изменяет картину течения жидкости. Поэтому вязкость неньютоновских жидкостей зависит не только от их природы и температуры, но и от градиента скорости их течения.
Ламинарное и турбулентное течение жидкости
Ламинарным называется такое течение жидкости, при котором она перемещается как бы слоями, каждый из которых характеризуется своей скоростью.
Именно такой вид течения был представлен на рис.6. При ламинарном течении жидкости в трубке круглого сечения она движется как бы коаксиальными цилиндрическими слоями, и все ее частицы перемещаются только параллельно оси трубки. Скорость течения максимальна в центре сечения трубки и уменьшается по направлению к ее стенками. Профиль распределения векторов скоростей в такой трубке показан на рис.7. Он представляет собой параболу.
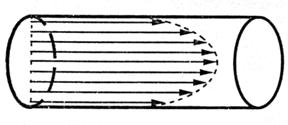
Рис. 7 Профиль распределения векторов скоростей жидкости
при ламинарном течении
Возможен и другой тип течения жидкости — турбулентное. При турбулентном течении скорости частиц жидкости беспорядочно меняются, в результате чего в потоке образуются местные завихрения, и ее частицы перемещаются не только параллельно, но и перпендикулярно оси трубки. В этих условиях происходит непрерывное перемешивание частиц жидкости.
Рейнольдс показал, что переход ламинарного течения жидкости в турбулентное зависит от ряда величин: вязкости жидкости 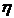 , ее плотности
, ее плотности 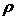 , скорости ее течения v и диаметра трубки D, Эти величины входят в уравнение Рейнольдса:
, скорости ее течения v и диаметра трубки D, Эти величины входят в уравнение Рейнольдса:
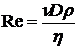
Re — безразмерная величина, так называемое число Рейнольдса. При малых значениях этого числа течение жидкости является ламинарным. Когда число Рейнольдса превышает некоторую критическую величину, ламинарное течение превращается в турбулентное. Для трубки круглого сечения такая величина числа Рейнольдса составляет примерно 2000.
Течение вязкой жидкости по трубкам. Уравнение Пуазейля
.
Хаген, изучая течение воды по трубкам, показал, что ее объемная
скорость пропорциональна четвертой степени радиуса трубок. Более подробно
исследовал это явление Пуазейль — автор важнейших работ по гидродинамике и физиологии кровообращения. Он установил экспериментально закон, характеризующий величину объемной скорости жидкости Q в трубках круглого сечения, и представил его в виде соответствующего уравнения, которое называют также основным уравнением гидродинамики.
Пусть жидкость, обладающая вязкостью  , течет по трубке с радиусом r (рис.8). Для того, чтобы определить ее объемную скорость Q , необходимо измерить разность давлений (полных) Р1 и Р2 на участке трубки длиной l.
, течет по трубке с радиусом r (рис.8). Для того, чтобы определить ее объемную скорость Q , необходимо измерить разность давлений (полных) Р1 и Р2 на участке трубки длиной l.
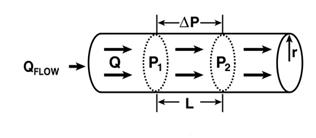
Рис. 8. Факторы, определяющие объемную скорость жидкости.
Величина объемной скорости Q определяется уравнением Пуазейля:
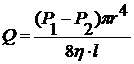
В соответствии с уравнением Пуазейля, объемная скорость
жидкости в трубке определяется разностью давлений в начале и конце трубки,
зависит от четвертой степени радиуса, а также от длины трубки и вязкости
жидкости:
Уравнение Пуазейля можно упростить и в то же время сделать его более универсальным, если ввести дополнительную величину R — гидродинамическое сопротивление:
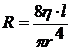
Тогда уравнение Пуазейля примет вид: 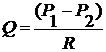 , или
, или 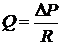
Использование понятия гидродинамического сопротивления расширяет рамки применения уравнения Пуазейля от единичной трубки круглого сечения до системы любой сложности, состоящей из многих трубок, соединенных последовательно или параллельно. Если не во всех случаях можно рассчитать гидродинамическое сопротивлении такой системы, то его можно, по крайней мере, измерить экспериментально.
Таким образом, смысл уравнения Пуазейля сводится к тому, что объемная скорость жидкости находится в прямой зависимости от разности давлений в начале и в конце трубки или системы трубок и в обратной зависимости от величины гидродинамического сопротивления.
Записанное в такой форме уравнение Пуазейля напоминает закон Ома для постоянного электрического тока. При этом объемная скорость жидкости аналогична силе тока, разность давлений — разности электрических потенциалов на концах проводника, а гидродинамическое сопротивление — электрическому сопротивлению. Это обстоятельство позволяет моделировать с помощью электрических цепей течение жидкости в трубках, в частности течение крови в сосудистой системе.
Необходимо отметить, что уравнение Пуазейля применимо только к ламинарному течению жидкости. В турбулентном потоке происходит более значительная убыль энергии, чем в ламинарном. Поэтому если развивается турбулентность, объемная скорость жидкости перестает отвечать уравнению Пуазейля. Ее величина становится приблизительно пропорциональной квадратному корню из разности давлений в начале и конце трубки.
Биофизические основы кровообращения
При каждой систоле сердце совершает работу А по приданию определенному объему крови V (систолическому объему) статического давления Р, а также по приданию массе крови m скорости 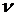 . Из этого следует, что работа как левого, так и правого желудочков сердца за один цикл составляет:
. Из этого следует, что работа как левого, так и правого желудочков сердца за один цикл составляет:
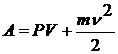
Поскольку величины Р и V меняются во времени, для получения точного значения А было бы необходимо проинтегрировать их. Однако задачу можно упростить, если взять их средние значения.
Из экспериментов известно, что средняя величина Р для левого желудочка составляет в покое приблизительно 100 мм рт. ст., а 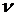 для аорты — 0,5 м/с. Величина V в покое равна в среднем 70мл. Подставив эти величины в приведенное выше уравнение, получим примерную величину работы левого желудочка за один сердечный цикл.
для аорты — 0,5 м/с. Величина V в покое равна в среднем 70мл. Подставив эти величины в приведенное выше уравнение, получим примерную величину работы левого желудочка за один сердечный цикл.
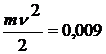 Дж
Дж
А = 0,931 Дж + 0,009 Дж
Таким образом, 99% работы левого желудочка сердца затрачивается на то, чтобы повысить давление в объеме крови, изгоняемом из него, и лишь 1% — на сообщение скорости этому объему крови. Соответственно, статическое давление в аорте составляет 99% полного давления, а динамическое — только 1% . Иначе говоря, основная часть удельной энергии крови в аорте является потенциальной и лишь очень малая часть – кинетической
Давление крови в легочной артерии значительно ниже, чем в аорте, а скорость крови примерно такая же. Подсчеты показывают, что для правого желудочка А = 0,15Дж.
Ламинарное течение жидкости в трубах различного сечения
Для начала рассмотрим установившееся ламинарное течение в круглых трубах.
В трубе диаметром 2∙r выделим цилиндрический объём жидкости между сечениями 1 и 2 длиной l и диаметром 2∙r. Отметим, что давления в сечениях 1 и 2 соответственно равны P1 и P2. Распределение скоростей по сечению потока на всей длине трубы одинаково, поэтому одинаково и значение коэффициента кинетической энергии α. На рассматриваемый объём, движущийся со скоростью υ, действуют силы давления (на торцовые поверхности) и силы сопротивления, вызванные вязким трением τ на боковой поверхности.
Теория ламинарного течения основывается на законе трения Ньютона, т.е. трение между слоями жидкости является единственным источником потерь энергии.
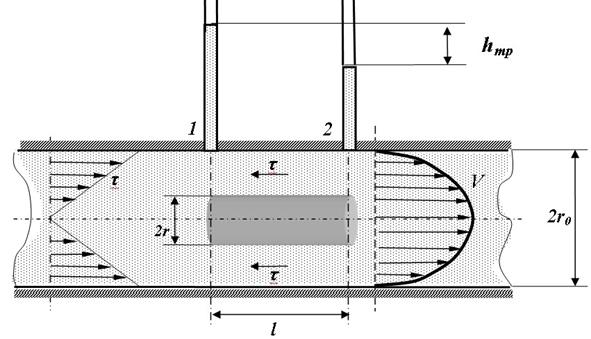
Рисунок 3.21 – Схема установившегося ламинарного течения
Уравнение Бернулли в данном случае может быть записано в виде
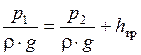 .
.
С учетом формулы расхода
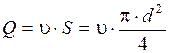
и зависимости коэффициента гидравлического трения от числа Рейнольдса при ламинарном движении
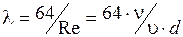
получим зависимость потерь в круглой трубе от расхода
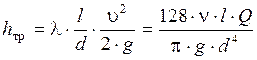 .
.
Эта формула выражает закон Пуазейля: при ламинарном течении жидкости в трубе круглого сечения потеря напора пропорциональна расходу и вязкости и обратно пропорциональна диаметру в четвертой степени.
Рассмотрим установившееся ламинарное течение в трубах с сечением в виде равностороннего треугольника. При течении жидкости в таких каналах для расчетов можно использовать следующие приближенные соотношения:
ü объемный расход жидкости 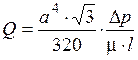 ;
;
ü потери давления на трение 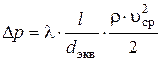 ;
;
ü эквивалентный диаметр сечения канала 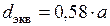 ;
;
ü закон сопротивления 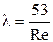 ;
;
ü число Рейнольдса 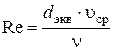 .
.
Рассмотрим установившееся ламинарное течение в трубах с сечением в виде квадрата. При течении жидкости в таких каналах для расчетов можно использовать следующие приближенные соотношения:
ü объемный расход жидкости  ;
;
ü потери давления на трение 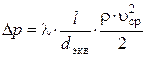 ;
;
ü эквивалентный диаметр сечения канала  ;
;
ü закон сопротивления 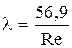 ;
;
ü число Рейнольдса 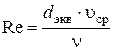 .
.
3.13.5 Местные гидравлические сопротивления
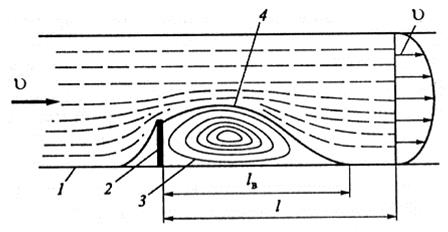
Рисунок 3.22 – Деформация потока при обтекании преграды: 1 – труба;
2 – преграда; 3 – водоворотная область; 4 – поверхность раздела.
При обтекании потоком какой-либо преграды (рисунок 3.22) происходит отрыв транзитной струи от стенки русла. При этом получаются области 3 – водоворотные зоны. При обтекании потоком местного сопротивления 2 искривляются линии тока, изменяется поле скоростей, может происходить отрыв потока, образуются области, заполненные мелкими и крупными вихрями (водоворотные зоны). В водоворотных зонах жидкость совершает интенсивные вращательные движения, поэтому потери энергии в этих зонах более интенсивны, чем в основном (транзитном) потоке. Местные сопротивления вызывают переход механической энергии потока в тепловую при преодолении касательных напряжений.
Местными гидравлическими сопротивлениями называются любые участки гидравлической системы, где имеются повороты, преграды на пути потока рабочей жидкости, расширения или сужения, вызывающие внезапное изменение формы потока, скорости или направления ее движения.
К местным гидравлическим сопротивлениям относятся: внезапное расширение трубопровода, внезапное сужение, постепенное расширение (диффузоры), постепенное сужение (конфузоры), колена, повороты, дроссельные шайбы, фильтрующие устройства, вентили, задвижки, клапаны и т.д.
Во многих случаях гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому местные потери напора можно определить по формуле Вейсбаха
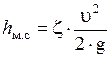 или
или 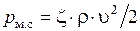 ,
,
где  – средняя скорость по сечению в трубе, в которой установлено местное сопротивление. Если же диаметр трубы и, следовательно, скорость в ней изменяются по длине, то за расчётную скорость принимают большую из скоростей.
– средняя скорость по сечению в трубе, в которой установлено местное сопротивление. Если же диаметр трубы и, следовательно, скорость в ней изменяются по длине, то за расчётную скорость принимают большую из скоростей.
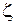 — коэффициент сопротивления, значение которого постоянно для данной формы местного сопротивления.
— коэффициент сопротивления, значение которого постоянно для данной формы местного сопротивления.
Если местные сопротивления расположены на близких расстояниях, и на разделяющем участке трубопровода эпюра  скоростей не успевает стабилизироваться, то происходит взаимное влияние сопротивлений. В этом случае общая потеря напора не будет равна сумме потерь напора на изолированных сопротивлениях. Взаимное влияние местных сопротивлений в трубопроводе становится заметным, если длина участка между ними l = (5¸6) d (d – внутренний диаметр трубопровода).
скоростей не успевает стабилизироваться, то происходит взаимное влияние сопротивлений. В этом случае общая потеря напора не будет равна сумме потерь напора на изолированных сопротивлениях. Взаимное влияние местных сопротивлений в трубопроводе становится заметным, если длина участка между ними l = (5¸6) d (d – внутренний диаметр трубопровода).
Из-за сложности структуры потока в области местного сопротивления коэффициенты местных сопротивлений определяют экспериментально.
Рассмотрим наиболее часто встречающееся местные сопротивления.
1) Внезапное расширение. При внезапном расширении потока в трубке жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы об основное русла потока 1, а также трение внутри вращающихся потоков 2, вследствие чего происходят существенные потери энергии. Кроме того, какая-то часть энергии жидкости затрачивается на фазовый переход частиц жидкости из основного потока во вращательные и наоборот.
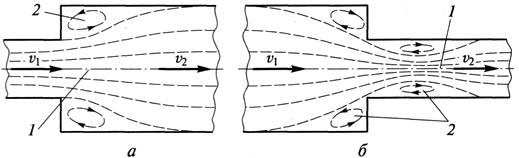
Рисунок 3.23 – Схемы внезапного расширения (а) и сужения (б) трубы:
1 – транзитный поток; 2 — вихревые области.
При внезапном расширении (рисунок 3.23, а) трубопровода потери напора можно определить по теореме Борда-Карно: потеря напора на внезапном расширении равна скоростному напору, определенному по разности скоростей или по формуле Борда с учетом уравнения неразрывности потока 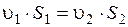 .
.
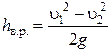 или
или 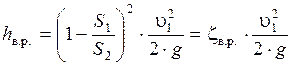
Когда площадь S2 значительно больше площади S1 (при выходе из трубы в резервуар), а скорость υ2 = 0, то теряется весь скоростной напор и потери можно определить по формуле
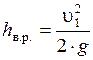 .
.
Т.о. при местном сопротивлении «выход из трубы в резервуар больших размеров» или «Выход из трубы под уровень» коэффициент местного сопротивления 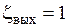 .
.
2) Внезапное сужение.Данное сопротивление вызывает меньшую потерю энергии чем внезапное расширение с таким же соотношением площадей (рисунок 3.23, б).
При внезапном сужении, так же как и при внезапном расширении потока, создаются пространства 2 с завихрениями вращающейся жидкости, которые образуются в пристенном пространстве широкой части трубы. Такие же завихрения образуются в начале узкой части трубы за счёт того, что при входе в неё (узкую часть) жидкость продолжает некоторое время двигаться по инерции в направлении центра трубы, и основное русло потока ещё некоторое время продолжает сужаться. Следовательно, при внезапном сужении потока возникает как — бы два подряд идущих местных сопротивления. Местное сопротивление за счёт сужения основного русла и сразу же за ним местное расширение, уже рассмотренное выше.
Потери определяются по формуле
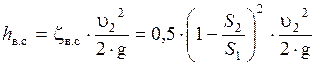 .
.
При входе в трубу из резервуара большого размера потери определяются как
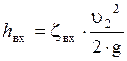 ,
,
где 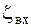 — коэффициент входа в трубу, определяется видом входной кромки.
— коэффициент входа в трубу, определяется видом входной кромки.
Для острых кромок 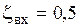 ; вход в трубу со скругленными кромками
; вход в трубу со скругленными кромками 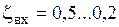 .
.
Дата добавления: 2015-04-19 ; просмотров: 3280 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ