Линейные неравенства с модулем примеры
Линейные неравенства с модулем примеры
Абсолютной величиной (модулем) называется функция, которая каждому числу
х R ставит в соответствие число
R ставит в соответствие число
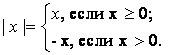
Величина |х| равна расстоянию от точки х до начала координат.
Пусть х и у — действительные числа. Приведем (в виде формул) свойства модуля.
1) |x| 0.
0.
2) |x| = 0 x = 0.
x = 0.
3) |x y| = |x|
y| = |x| |y|.
|y|.
4) |x : y| = |x| : |y|, где у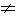 0 .
0 .
5)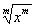 = |x|, где m — четное число (2, 4, 6. ).
= |x|, где m — четное число (2, 4, 6. ).
6) |x| n = x n , где n — четное число (2, 4, 6. ).
7) |x + y| |x| + |y|.
|x| + |y|.
8) |x — y| |x| — |y|.
|x| — |y|.
1. Стандарный способ.
Стандарный способ решения неравенств, содержащих модуль, состоит в том, что, зная промежутки, на которых функция, находящая под знаком модуля принимает значения определенных знаков, снимают знак модуля.
В общем случае при решении неравенств этим способом поступают так:
а) Находят ОДЗ неравенства.
б) Находят точки в которых функции, стоящие под знаком модуля, равны 0.
в) Полученные точки разделяют ОДЗ на несколько множеств.
г) На каждом, из полученных множеств, определяют знак каждой функци и, согласно определению модуля, снимают знак модуля.
д) Решают каждое из полученных неравенств.
е) Полученные множества объединяют.
Задача 1. Решить неравенство |x 2 — 3x + 2| + |2x +1| 2 — 3x + 2 = 0;
Три числа -0,5; 1 и 2 разделяют множество действительных чисел на четыре множества. Поэтому рассмотрим четыре случая.
1) (- ; -0,5]. На этом промежутке x 2 — 3x + 2 > 0, 2x + 1 2 — 3x + 2 -2x — 1 2 — 5x — 4 0, следовательно, x1 =
; -0,5]. На этом промежутке x 2 — 3x + 2 > 0, 2x + 1 2 — 3x + 2 -2x — 1 2 — 5x — 4 0, следовательно, x1 = ; x1 =
; x1 = ;;
;;
 x
x -0,5,
-0,5,
 2 — 3x + 2 > 0, 2x + 1 > 0,
2 — 3x + 2 > 0, 2x + 1 > 0,
тогда x 2 — 3x + 2 + 2x + 1 2 — x — 2 0, x1 = -1; x2 = 2;
 -0,5 2 — 3x + 2 0;
-0,5 2 — 3x + 2 0;
-x 2 + 3x — 2 + 2x + 1 > 5;
D =25 — 24 = 1 > 0, x1 = 2; x2 = 3;
 1 3;
1 3;
Решение этого неравенства на этом промежутке x (1; 2)
(1; 2)
4) (2; + ). . На этом промежутке x 2 — 3x + 2 > 0, 2x + 1 > 0;
). . На этом промежутке x 2 — 3x + 2 > 0, 2x + 1 > 0;
x 2 — 3x + 2 + 2x + 1 2 — x — 2 2,
-1 g(x) ( , 0
, 0
Рекомендуем читателю построить график функции y = |f(x)| и обдумать формулы, а заодно и каждую строчку приведенной таблицы.
Пример 2. Решить неравенство |х + 5| > 4.
ОДЗ: х R. Согласно восьмой строке таблицы
R. Согласно восьмой строке таблицы
|x + 5| > 4 x + 5 4
x + 5 4 x -1.
x -1.
Ответ: х (-
(- ; -9)
; -9) (-1; +
(-1; + ).
).
Пример 3. Решить неравенство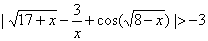 .
.
Решим систему неравенств
 17 + x
17 + x 0,
0,
8 — x 0;
0;
 x
x -17,
-17,
x 8;
8;
Таким образом ОДЗ функции, стоящей в левой части неравенства, является множество чисел из промежутка [-17; 0) (0; 8]. На этом множестве левая часть неравенства неотрицательна, следовательно, решением данного неравенства является ОДЗ.
(0; 8]. На этом множестве левая часть неравенства неотрицательна, следовательно, решением данного неравенства является ОДЗ.
Ответ: [-17; 0) (0; 8].
(0; 8].
Пример 4. Решить неравенство |x 2 -6x + 5| x + 5.
x + 5.
Это неравенство равносильно совокупности неравенств
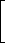 x 2 — 6x + 5
x 2 — 6x + 5 x + 5,
x + 5,
x 2 — 6x + 5 -x — 5;
-x — 5;
Упростим каждое из неравенств полученной совокупности
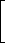 x 2 — 7x
x 2 — 7x 0,
0,
x 2 — 5x + 10 0;
0;
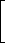 x(х — 7)
x(х — 7) 0,
0,
x 2 — 5x + 10 0;
0;
Решением первого неравенства является множество чисел (- ; 0]
; 0] [7; +
[7; + ).
).
Квадратный трехчлен x 2 — 5x + 10 имеет отрицательный дискриминант, поэтому принимает только положительные значения и, следовательно, второе неравенство решений не имеет.
Ответ: (- ; 0]
; 0] [7; +
[7; + ).
).
2). В ряде случаев (например, если g(х) — квадратный корень либо абсолютная величина, либо любая непрерывная функция, принимающая на всей области определения неотрицательные значения), рассматриваемые неравенства удобнее всего решать возведением в квадрат. Как и в неравенствах |f  ,
, 1, 0. Для тех х из ОДЗ, где g(х) » выбран для определенности).
1, 0. Для тех х из ОДЗ, где g(х) » выбран для определенности).
Алгоритм решения неравенства|f
1.Почленно возвести в квадрат|f(x)| 2 > (g(x)) 2 , используя свойство 6, получим неравенство равносильное данному(f
3.Воспользоваться формулой(f(x) — g(х)) (f(x) + g(x)) > 0
4.Применить метод интервалов
Пример 5. Решить неравенство |x 2 — 5x + 9| 2 — 5x + 9| 2 2 .
(x 2 — 5x + 9) 2 — (x — 6) 2 2 — 5x + 9 -(x — 6))(x 2 — 5x + 9 +(x — 6)) 2 — 6x + 15)(x 2 — 4x + 3) 2 — 6x + 15 отрицателен (6 2 — 60 = -24) поэтому на всей области определения он принимает только положительные значения.
Дискриминант квадратного трехчлена x 2 — 4x + 3 положителен (4 2 — 12 = 4), он имеет два корня и они равны 1 и 3. Отрицательные значения квадратный трехчлен принимает, если 1
Решение неравенств с модулями
















Описание презентации по отдельным слайдам:
Неравенства с модулями 11 класс презентация—— Абрамова Светлана Ивановна
Решить неравенство : |3 — 8×2| > -3 Решение. Поскольку модуль всегда заведомо больше отрицательного числа, решением этого неравенства является область определения функции, стоящей под знаком модуля, т.е. любое рациональное число. http://presentation-creation.ru/
Решить неравенство: |x2 — 2x| ≤ 0 Решением этого неравенства будут корни уравнения x2-2x=0 ,т.е. x1=0 и x2=2. Ответ : x ϵ <0>ᴜ <2>Решить неравенство : |7×2 + 8| ≤ -3 Неравенство решений не имеет, так как модуль всегда положителен. Решение. Решение.
Решить неравенство : |x2 — 7x| ≥ 12 Решение. Равносильные неравенства x2 — 7x ≥ 12 и x2 — 7x ≤ -12 сводятся к квадратным x2 — 7x -12 ≥ 0 и x2 — 7x + 12 ≤ 0. Решаем первое неравенство. Решаем второе неравенство. Следовательно, решением исходного неравенства будут три интервала решений квадратных неравенств. http://presentation-creation.ru/
Решение. (6x – 8)(x – 3) ≥ 0 x ≠ 3 x – 3 3 — x сводится к решению двух равносильных неравенств : x2 — 9x + 18 0 x1 = 3 x2 = 6 x1 = 3 x2 = 4 x ϵ ( 3 ; 6 ) x ϵ ( -∞ ; 3) ᴜ ( 4 ; ∞ ) Ответ : x ϵ ( 4 ; 6 ) 3 3 4 6
Решить неравенство : |x — 4|3 + |x — 4|> 2 Решение . Заменой y=|x — 4| исходное неравенство сводится к равносильной системе : y 3 + y > 2 y ≥ 0 y3 + y – 2 y3 – y2 y2 + y y2 – y 2у – 2 2у – 2 y — 1 y2 + y + 2 0 — — — Первое неравенство y 3 + y — 2 > 0 – рациональное. Решать его нужно методом интервалов для рациональных и дробно-рациональных неравенств, предварительно разложив левую часть на множители. Корень у=1 кубического трехчлена угадывается сразу. Поэтому, деля y 3 + y — 2 на у – 1 или применяя метод неопределенных коэффициентов с использованием теоремы Безу, разложим выражение на два сомножителя – линейный и квадратный. Click to add title
Неравенства вида |f(x)|>|g(x)|, как и соответствующие уравнения, сводятся к равносильному [ f(x) ]2 > [ g(x) ]2 .
Решить неравенство : |2x — 5| — |4x + 7|≥ 0 Решение . Приводим исходное неравенство к виду |2x — 5| ≥ |4x + 7| и возводим в квадрат : (2x – 5)2 ≥ (4x + 7)2 Раскрывая скобки и приводя подобные члены, получаем квадратное неравенство : 3×2 + 19x + 6 ≤ 0 3×2 + 19x + 6 = 0
Неравенства вида |f1(x)|±|f2(x)|±…±|fn(x)| v a решаются тем же самым методом интервалов, что и уравнения с модулем. Разница лишь в том, что в данном случае в каждом интервале решается не уравнение, а неравенство и из решений неравенства выбираются те, которые принадлежат данному интервалу. В остальном метод интервалов остается тем же, что и при решении уравнений с модулем. Не следует путать этот метод с методом интервалов, применяемым для решения рациональных и дробно-рациональных неравенств. Внимание! Click to add title
Решить неравенство : |x|- 2|x + 1|+ 3|x + 2|≥ 4 Решение . Найдем сначала все xi , разбивающие числовую ось на интервалы и получающиеся как решения уравнений fj (xi )=0 : х=0; х + 1=0 ; х + 2=0. Таким образом, границами интервалов являются числа x1=0, x2=-1 и x3=-2. Отметим эти значения на числовой оси для каждого из полученных интервалов определим знаки выражений, стоящих под знаком модуля : I II III IV -2 -1 0 x 0 x 0 x + 2 > 0 x>0 x + 1 > 0 x + 2 > 0 Раскроем модули на интервале I (x≤-2) : -x + 2( + 1) – 3(x + 2) ≥ 4 После преобразования получаем -2х – 4 ≥ 4 , откуда х ≤ -4 Click to add title
Этот интервал входит в интервал I и является решением исходного неравенства. II интервал ( -2≤ х ≤-1 ) : -х+ 2(х + 1) + 3(х + 2) ≥ 4 4х + 8 ≥ 4 , откуда х≥-1 Решением в этом интервале является точка х=-1 III интервал ( -1≤ х ≤0 ) : -х – 2(х + 1) + 3(х + 2) ≥ 4 4 ≥ 4 В результате мы получили истинное неравенство ( заметим, что, если бы неравенство было строгим, оно становилось бы ложным). Следовательно, весь интервал III является решением исходного неравенства. IV интервал ( х≥0 ) х – 2(х + 1) + 3( + 2) ≥ 4 2х + 4 ≥ 4 , откуда х≥0 Ответ : ( -∞ ; -4 ] ᴜ [ -1 ; ∞ ) Click to add title
! Презентация составлена учителем математики Абрамовой С.И. К элективному курсу 11 класс по теме « Решение Неравенств модулями» 24.12.18г Click to add title
Click to add title
Выберите книгу со скидкой:

Для детского сада. Математика. Средняя группа
350 руб. 144.00 руб.

Математика. Сложение и вычитание. Уровень 3 Kumon
350 руб. 464.00 руб.

Математика. Дроби. Уровень 4 Kumon
350 руб. 464.00 руб.

Альбом по подготовке к школе. Математика
350 руб. 272.00 руб.

Для детского сада. Математика. Старшая группа
350 руб. 144.00 руб.

Для детского сада. Математика. Подготов. группа
350 руб. 144.00 руб.

Для детского сада. Математика. Младшая группа
350 руб. 144.00 руб.

Непоседа. Нескучная математика
350 руб. 109.00 руб.

6-7 лет. Математика. Проверяем готовность к школе
350 руб. 181.00 руб.

Математика. Деление. Уровень 4 Kumon
350 руб. 464.00 руб.

Математика. Готовлюсь к школе с наклейками
350 руб. 130.00 руб.

Математика. Умножение. Уровень 4 Kumon
350 руб. 464.00 руб.
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА
Инфолавка — книжный магазин для педагогов и родителей от проекта «Инфоурок»




Решение неравенств с модулями является одной из сложных тем, которая включена в ЕГЭ по математике, поэтому данную тему я рассматриваю на уроках при изучении темы неравенств а так же и на элективном курсе.
Неравенства решаются тем же самым методом интервалов, что и уравнения с модулем. Разница лишь в том, что в данном случаев каждом интервале решается не уравнение, а неравенство и из решений неравенства выбираются те, которые принадлежат данному интервалу. В остальном метод интервалов остается тем же, что и при решении уравнений с модулем.
- Абрамова Светлана Ивановна
- Написать
- 09.01.2019
Номер материала: ДБ-349231
Добавляйте авторские материалы и получите призы от Инфоурок
Еженедельный призовой фонд 100 000 Р



«Развитие эмоционального интеллекта»
Спикер: Анна Быкова (#лениваямама)
- 08.01.2019
- 221
- 08.01.2019
- 96
- 07.01.2019
- 96
- 07.01.2019
- 176
- 07.01.2019
- 168
- 06.01.2019
- 239
- 06.01.2019
- 179
- 06.01.2019
- 218
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Методы решения уравнений и неравенств с модулем

Методы решения уравнений и неравенств с модулем
Цели. Целью моей работы является классификация методов решения уравнений и неравенств, содержащих переменную под знаком модуля (абсолютной величины). Данное исследование возникло из необходимости обобщить все знания по этой теме для проникающего повторения при подготовке к Единому Государственному Экзамену в 10 – 11 классах. В результате исследования мне удалось выделить три основных метода, которые являются универсальными для решения уравнений (неравенств) своего типа, а так же, были выявлены частные случаи этих методов, упрощающие общую схему решения.
Считаю, что данная работа будет полезна ученикам 11-х классов.
Типы уравнений (неравенств) и методы их решения:
I. Простейшие – уравнения и неравенства вида
|f(x)| = a, |f(x)| a, где а – любое число.
При решении простейших уравнений и неравенств исходим из определения модуля, как расстояния от нуля до числа, выраженного в единичных отрезках.
1. Рассмотрим уравнения вида | f(x)| = a:
Решение неравенства – множество значений f(х) «между» числами а и – а:
двойное неравенство — a а ( ):
):
б). Если а = 0, то |f(x)| > 0. Тогда  , т. к. |f(x)|
, т. к. |f(x)|  0.
0.
(|f(x)| 0. Решение:
0. Решение:  (см. выше)).
(см. выше)).

|f(x)| > a 
 Решение неравенства: множество значений х «за» числами а и – а.
Решение неравенства: множество значений х «за» числами а и – а.
1.| x+2| = 3 



2.








Ответ: x = 3, x = -1.
3.
 , тогда
, тогда  или
или








 .
.
Ответ: (-∞;1  ).
).
4. | x2 +5x | ≥ 6, 





Ответ: (-∞;-6] [-3;-2]
[-3;-2]  [1;+ ∞).
[1;+ ∞).
- |f(x)| = f(x)
 f(x) ≥ 0 Решение уравнения – решение неравенства. |f(x)| = — f(x)
f(x) ≥ 0 Решение уравнения – решение неравенства. |f(x)| = — f(x)  f(x) ≤ 0. |f(x)|=|g(x)|
f(x) ≤ 0. |f(x)|=|g(x)| 

1.





 x = 1, x =3.
x = 1, x =3.
2.| x2 – 1| = (x – 1)(x + 1),

Ответ: (-∞; — 1]  [1;+ ∞).
[1;+ ∞).
II. По определению модуля.
Если в уравнении или неравенстве один модуль и функция (|f(x)| * g(x)), то решаем по определению модуля:
|f(x)|= 
Для этого нужно рассмотреть два случая, раскрывая модуль, в зависимости от знака подмодульного выражения Изменения происходят только в части, содержащей модуль.
1. 2|x +1|>x+4, 





Ответ: 
2. 







Ответ: x = 1, x = — 

Данное равенство возможно, только если  . Тогда:
. Тогда:
 Только для уравнений, в которых g(x) проще f(x).
Только для уравнений, в которых g(x) проще f(x).
1. 





Ответ: x = 1, x = 6.
III. Метод интервалов
А) В случае, когда в уравнении или неравенстве сумма (разность) нескольких модулей.
1.
1.Приведем подмодульные выражения к виду ax + b, где a > 0, по свойству  .
.  .
.
2.Найдем нули модулей: х = — 1, х = 4.
3.Отметим нули модулей на числовом луче и выделим числовые промежутки.
4.Заполним таблицу и расставим знаки, используя свойство линейной функции y = kx + b при k>0 (возрастающая функция, при переходе через ноль знак меняется с « — » на « + »).
Неравенство с двумя модулями. Часть II
«Неравенство с двумя модулями. Часть I» смотрим здесь.
Решим неравенство
Правило раскрытия модуля говорит, что раскрытие модуля зависит от того, какой знак имеет подмодульное выражение. Стало быть, нас будут интересовать нули подмодульных выражений, – смена знака подмодульного выражения возможна только в них.
В нашем случае нуль первого модуля – это 4, нули второго подмодульного выражения – это -3 и 2.
Вся числовая ось указанными точками разбивается на 4 промежутка. Нам предстоит поработать с неравенством в каждом из них.
Если у вас возник вопрос, почему, например, в крайнем левом промежутке у нас число -3 не включено, а на следующем включено (аналогично с другими), – ответим на него. На самом деле, – все равно, куда именно вы включите концы промежутков. Лишь бы при склейке все промежутки давали бы нам всю числовую прямую, если мы работаем на R.

Выясним, как распределяются знаки подмодульных выражений на каждом из промежутков.
Начнем с первого подмодульного выражения. Очевидно, что при 4″ title=»Rendered by QuickLaTeX.com» height=»15″ width=»48″ style=»vertical-align: -1px;»/> знак выражения
– минус, то есть
, а при
.

«Переключателями» же знака второго подмодульного выражения из неравенства являются точки -3 и 2. Если , то
при остальных
имеем:
0″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»127″ style=»vertical-align: -2px;»/>. Если вам не кажутся очевидными знаки этого подмодульного выражения на указанных промежутках, загляните сюда (метод интервалов).

Мы замечаем, что на двух промежутках (первом и третьем слева) знаки подмодульных выражений распределены одинаково.
Итак, первый случай:
Предстоит решить систему (мы объединили первый и третий промежутки в совокупность):
Во второй строке системы приводим подобные слагаемые и раскладываем на множители:
Теперь переходим на ось, пересекаем два множества между собой:

.
Второй случай:

.
Третий случай:
4,& & -4+x+x^2+x-6geq 7; end
4,& & x^2+2x-17geq 0; end
4,& & (x-(-1+3sqrt2))(x-(-1-3sqrt2))geq 0; end

.
Нам осталось объединить решения каждого из случаев между собой:

Ответ:
Для тренировки предлагаю Вам решить следующее неравенство:



