Логарифмические неравенства Гипермаркет знаний
Логарифмические неравенства — Гипермаркет знаний
С ними находятся внутри логарифмов.
Как решать логарифмические неравенства:
Любое логарифмическое неравенство нужно стремиться привести к виду (log_a
Но при выполнении этого перехода есть одна очень важная тонкость:
(-) если — число и оно больше 1 — знак неравенства при переходе остается прежним,
(-) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
Очень важно! В любом неравенстве переход от вида (log_a <f(x)>˅ log_a
Пример . Решить неравенство: (log)(≤-1)
Раскрываем скобки, приводим .
Умножаем неравенство на (-1), не забыв при этом перевернуть знак сравнения.
Построим числовую ось и отметим на ней точки (frac<7><3>) и (frac<3><2>) . Обратите внимание, точка из знаменателя – выколота, несмотря на то, что неравенство нестрогое. Дело в том, что эта точка не будет решением, так как при подстановке в неравенство приведет нас к делению на ноль.

(x∈()(frac<3><2>) (;)(frac<7><3>])
Теперь на ту же числовую ось наносим ОДЗ и записываем в ответ тот промежуток, который попадает в ОДЗ.

Записываем окончательный ответ.
Пример . Решить неравенство: (log^2_3x-log_3x-2>0)
Приступим к решению.
Перед нами типичное квадратно-логарифмическое неравенство. Делаем .
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к , имеющей такое же решение, и сделаем обратную замену.
(left[ begin
Эти четыре неравенства составляют систему и должны выполняться одновременно. Когда область допустимых значений найдена, остается пересечь ее с решением рационального неравенства — и ответ готов.
Задача. Решите неравенство:
Для начала выпишем ОДЗ логарифма:
Первые два неравенства выполняются автоматически, а последнее придется расписать. Поскольку квадрат числа равен нулю тогда и только тогда, когда само число равно нулю, имеем:
x 2 + 1 ≠ 1;
x 2 ≠ 0;
x ≠ 0.
Получается, что ОДЗ логарифма — все числа, кроме нуля: x ∈ (−∞ 0)∪(0; +∞). Теперь решаем основное неравенство:

Выполняем переход от логарифмического неравенства к рациональному. В исходном неравенстве стоит знак «меньше», значит полученное неравенство тоже должно быть со знаком «меньше». Имеем:
(10 − (x 2 + 1)) · (x 2 + 1 − 1)
Задача. Решите неравенство:
Найдем область определения (ОДЗ) первого логарифма:
Решаем методом интервалов. Находим нули числителя:
Затем — нули знаменателя:
Отмечаем нули и знаки на координатной стреле:

Получаем x ∈ (−∞ 2/3)∪(1; +∞). У второго логарифма ОДЗ будет таким же. Не верите — можете проверить. Теперь преобразуем второй логарифм так, чтобы в основании стояла двойка:
Как видите, тройки в основании и перед логарифмом сократились. Получили два логарифма с одинаковым основанием. Складываем их:

Неравенство называется логарифмическим, если в нём содержится логарифмическая функция.
Методы решения логарифмических неравенств не отличаются от , за исключением двух вещей.
Во-первых, при переходе от логарифмического неравенства к неравенству подлогарифмических функций следует следить за знаком получающегося неравенства . Он подчиняется следующему правилу.
Если основание логарифмической функции больше $1$, то при переходе от логарифмического неравенства к неравенству подлогарифмических функций знак неравенства сохраняется, а если же меньше $1$, то меняется на противоположный.
Во-вторых, решение любого неравенства – промежуток, а, значит, в конце решения неравенства подлогарифмических функций необходимо составить систему из двух неравенств: первым неравенством этой системы будет неравенство подлогарифмических функций, а вторым – промежуток области определения логарифмических функций, входящих в логарифмическое неравенство.
Практика.
Основание логарифма равно $2>1$, поэтому знак не меняется. Пользуясь определением логарифма, получим:
Логарифмические неравенства
Содержание
Логарифмические неравенства
На предыдущих уроках мы с вами познакомились с логарифмическими уравнениями и теперь знаем, что это такое и как их решать. А сегодняшний урок будет посвящен изучению логарифмических неравенств. Что же это за такие неравенства и в чем разница между решением логарифмического уравнения и неравенства?
Логарифмические неравенства — это неравенства, которые имеют переменную, стоящую под знаком логарифма или в его основании.
Или же, можно еще сказать, что логарифмическое неравенство – это такое неравенство, в котором его неизвестная величина, как и в логарифмическом уравнении, будет стоять под знаком логарифма.
Простейшие логарифмические неравенства имеют такой вид:
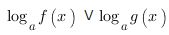
где f(x) и g(x) являются некоторыми выражениями, которые зависят от x.
Давайте это рассмотрим на таком примере: f(x)=1+2x+x2, g(x)=3x−1.
Решение логарифмических неравенств
Перед решением логарифмических неравенств, стоит отметить, что они при решении имеют сходство с показательными неравенствами, а именно:
• Во-первых, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, нам также необходимо сравнить основание логарифма с единицей;
• Во-вторых, решая логарифмическое неравенство, используя замену переменных, нам необходимо решать неравенства относительно замены до того момента, пока мы не получим простейшее неравенство.
Но это мы с вами рассмотрели сходные моменты решения логарифмических неравенств. А сейчас обратим внимание на довольно таки существенное отличие. Нам с вами известно, что логарифмическая функция обладает ограниченной областью определения, поэтому переходя от логарифмов к выражениям, стоящим под знаком логарифма, нужно брать в расчет область допустимых значений (ОДЗ).
То есть, следует учитывать, что решая логарифмическое уравнение мы с вами, можем сначала находить корни уравнения, а потом делать проверку этого решения. А вот решить логарифмическое неравенство так не получится, поскольку переходя от логарифмов к выражениям, стоящим под знаком логарифма, необходимо будет записывать ОДЗ неравенства.
Вдобавок стоит запомнить, что теория неравенств состоит из действительных чисел, которыми являются положительные и отрицательные числа, а также и число 0.
Например, когда число «а» является положительным, то необходимо использовать такую запись: a >0. В этом случае, как сумма, так и произведение таких этих чисел также будут положительными.
Основным принципом решения неравенства является его замена на более простое неравенство, но главное, чтобы оно было равносильно данному. Дальше, также мы получили неравенство и снова его заменили на то, которое имеет более простой вид и т.д.
Решая неравенства с переменной нужно находить все его решения. Если два неравенства имеют одну переменную х, то такие неравенства равносильны, при условии, что их решения совпадают.
Выполняя задания на решение логарифмических неравенств, необходимо запомнить, что когда a > 1, то логарифмическая функция возрастает, а когда 0 , ≤ или ≥.
Когда основание данного логарифма больше единицы (a>1), осуществляя переход от логарифмов к выражениям, стоящим под знаком логарифма, то в этом варианте знак неравенства сохраняется, и неравенство будет иметь такой вид:
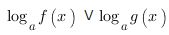
что равносильно такой вот системе:
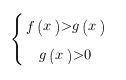
В случае же, когда основание логарифма больше нуля и меньше единицы (0
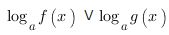
Это равносильно данной системе:
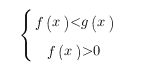
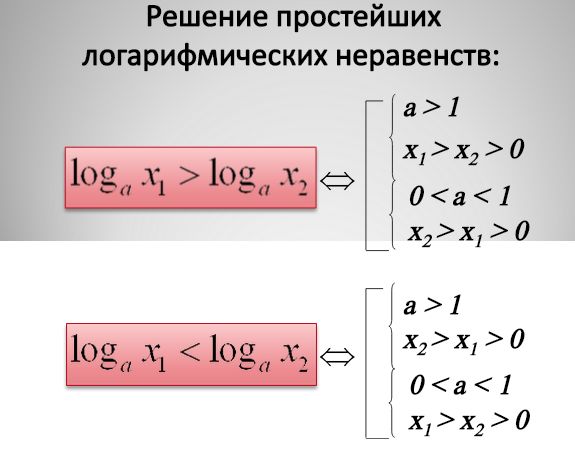
Посмотрим еще примеры решения простейших логарифмических неравенств, приведенных на картинке ниже:
Решение примеров
Задание. Давайте попробуем решить такое вот неравенство:
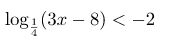
Решение области допустимых значений.
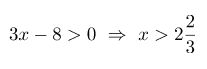
Теперь попробуем умножить его правую часть на:
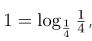
Смотрим, что у нас получится:
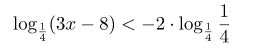
Далее, следуя свойствам логарифмов, возьмем и внесем коэффициент –2, как степень подлогарифмического выражения и в итоге получим:
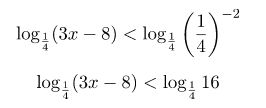
Теперь, давайте с вами перейдем к преобразованию подлогарифмических выражений. В связи с тем, что основание логарифма 0 16;
3x > 24;
х > 8.
А из этого следует, что интервал, который мы получили, целиком и полностью принадлежит ОДЗ и является решением такого неравенства.
Вот какой ответ у нас получился:
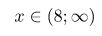
Что необходимо для решения логарифмических неравенств?
А теперь давайте попробуем проанализировать, что нам необходимо для успешного решения логарифмических неравенств?
• Во-первых, сосредоточить все свое внимание и постараться не допускать ошибок при выполнении преобразований, которые даны в этом неравенстве. Также, следует запомнить, что при решении таких неравенств нужно не допускать расширений и сужений ОДЗ неравенства, которые могут привести к потере или приобретению посторонних решений.
• Во-вторых, при решении логарифмических неравенств необходимо научиться мыслить логически и понимать разницу между такими понятиями, как система неравенств и совокупность неравенств, чтобы вы без проблем смогли осуществлять отбор решений неравенства, при этом руководствуясь его ОДЗ.
• В-третьих, для успешного решения таких неравенств каждый из вас должен отлично знать все свойства элементарных функций и четко понимать их смысл. К таким функциям относятся не только логарифмические, но и рациональные, степенные, тригонометрические и т.д., одним словом, все те, которые вы изучали на протяжении школьного обучения алгебры.
Как видите, изучив тему о логарифмических неравенствах, в решении этих неравенств нет ничего сложного при условии, если вы будете внимательны и настойчивы в достижении поставленных целей. Чтобы в решении неравенств не возникало никаких проблем, нужно как можно больше тренироваться, решая различные задания и при этом запоминать основные способы решения таких неравенств и их систем. При неудачных решениях логарифмических неравенств, следует внимательно проанализировать свои ошибки, чтобы в будущем не возвращаться к ним снова.
Домашнее задание
Для лучшего усвоения темы и закрепления пройденного материала, решите следующие неравенства:
Как решать логарифмические неравенства егэ. Логарифмические неравенства — Гипермаркет знаний
Логарифмы были придуманы для ускорения и упрощения вычислений. Идея логарифма, т. е. идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю. Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития. Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским учёным Джоном Непером(1550-1617) и швейцарцем Иобстом Бюрги(1552-1632) Первым опубликовал работу Непер в 1614г. под названием «Описание удивительной таблицы логарифмов», теория логарифмов Непера была дана в достаточно полном объёме, способ вычисления логарифмов дан наиболее простой, поэтому заслуги Непера в изобретении логарифмов больше, чем у Бюрги. Бюрги работал над таблицами одновременно с Непером, но долгое время держал их в секрете и опубликовал лишь в 1620г. Идеей логарифма Непер овладел около1594г. хотя таблицы опубликовал через 20 лет. Вначале он называл свои логарифмы «искусственными числами» и уже потом предложил эти «искусственные числа» называть одним словом «логарифм», который в переводе с греческого- «соотнесённые числа», взятые одно из арифметической прогресси, а другое из специально подобранной к ней геометрической прогресси. Первые таблицы на русском языке были изданы в1703г. при участии замечательного педагога 18в. Л. Ф Магницкого. В развитии теории логарифмов большое значение имели работы петербургского академика Леонарда Эйлера. Он первым стал рассматривать логарифмирование как действие, обратное возведению в степень, он ввёл в употребление термины «основание логарифма» и «мантисса» Бригс составил таблицы логарифмов с основанием 10. Десятичные таблицы более удобны для практического употребления, теория их проще, чем у логарифмов Непера. Поэтому десятичные логарифмы иногда называют бригсовыми. Термин «характеристика» ввёл Бригс.
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
Логарифмические уравнения и неравенства
1. Логарифмические уравнения
Уравнение, содержащее неизвестное под знаком логарифма или в его основании, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение вида
Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = a b .
Пример 1. Решить уравнения:
a) log 2 x = 3, b) log 3 x = -1, c)
Решение. Используя утверждение 1, получим a) x = 2 3 или x = 8; b) x = 3 -1 или x = 1 / 3 ; c)
Приведем основные свойства логарифма.
Р1. Основное логарифмическое тождество:

Р2. Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей:
Замечание. Если N 1 ·N 2 > 0, тогда свойство P2 примет вид
Р3. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя
 (a > 0, a ≠ 1, N 1 > 0, N 2 > 0).
(a > 0, a ≠ 1, N 1 > 0, N 2 > 0).
, (что равносильно N 1 N 2 > 0) тогда свойство P3 примет вид  (a > 0, a ≠ 1, N 1 N 2 > 0).
(a > 0, a ≠ 1, N 1 N 2 > 0).
P4. Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа:
Замечание. Если k — четное число (k = 2s ), то
P5. Формула перехода к другому основанию:
 (a > 0, a ≠ 1, b > 0, b ≠ 1, N > 0),
(a > 0, a ≠ 1, b > 0, b ≠ 1, N > 0),
в частности, если N = b , получим
Используя свойства P4 и P5, легко получить следующие свойства
 (a > 0, a ≠ 1, b > 0, c ≠ 0), (3) (a > 0, a ≠ 1, b > 0, c ≠ 0), (4)
(a > 0, a ≠ 1, b > 0, c ≠ 0), (3) (a > 0, a ≠ 1, b > 0, c ≠ 0), (4)  (a > 0, a ≠ 1, b > 0, c ≠ 0), (5)
(a > 0, a ≠ 1, b > 0, c ≠ 0), (5)
и, если в (5) c — четное число (c = 2n ), имеет место
 (b > 0, a ≠ 0, |a | ≠ 1). (6)
(b > 0, a ≠ 0, |a | ≠ 1). (6)
Перечислим и основные свойства логарифмической функции f (x ) = log a x :
1. Область определения логарифмической функции есть множество положительных чисел.
2. Область значений логарифмической функции — множество действительных чисел.
3. При a > 1 логарифмическая функция строго возрастает (0 log a x 2).
4. log a 1 = 0 и log a a = 1 (a > 0, a ≠ 1).
5. Если a > 1, то логарифмическая функция отрицательна при x (0;1) и положительна при x (1;+∞), а если 0 1, то логарифмическая функция выпукла вверх, а если a (0;1) — выпукла вниз.
Следующие утверждения (см., например, ) используются при решении логарифмических уравнений.
С ними находятся внутри логарифмов.
Как решать логарифмические неравенства:
Любое логарифмическое неравенство нужно стремиться привести к виду (log_a
Но при выполнении этого перехода есть одна очень важная тонкость:
(-) если — число и оно больше 1 — знак неравенства при переходе остается прежним,
(-) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
Логарифмические уравнения неравенства системы. Логарифмические неравенства — Гипермаркет знаний
- 1 уровень – научить решать простейшие логарифмические неравенства, применяя определение логарифма, свойства логарифмов;
- 2 уровень – решать логарифмические неравенства, выбирая самостоятельно способ решения;
- 3 уровень – уметь применять знания и умения в нестандартных ситуациях.
Развивающие: развивать память, внимание, логическое мышление, навыки сравнения, уметь обобщать и делать выводы
Воспитательные: воспитывать аккуратность, ответственность за выполняемое задание, взаимопомощь.
Методы обучения: словесный, наглядный, практический, частично-поисковый, самоуправления, контроля.
Формы организации познавательной деятельности учащихся: фронтальный, индивидуальный, работа в парах.
Оборудование: набор тестовых заданий, опорный конспект, чистые листы для решений.
Тип урока: изучение нового материала.
1. Организационный момент. Объявляются тема и цели урока, схема проведения урока: каждому ученику выдается оценочный лист, который ученик заполняет в течении урока; для каждой пары учеников – печатные материалы с заданиями, выполнять задания нужно в парах; чистые листы для решений; опорные листы: определение логарифма; график логарифмической функции, ее свойства; свойства логарифмов; алгоритм решения логарифмических неравенств.
Все решения после самооценки сдаются учителю.
Оценочный лист учащегося
2. Актуализация знаний.
Указания учителя. Вспомните определение логарифма, график логарифмической функции и ее свойства. Для этого прочитайте текст на с.88–90, 98–101 учебника “Алгебра и начала анализа 10–11” под редакцией Ш.А Алимова, Ю.М Колягина и др.
Ученикам раздаются листы, на которых записаны: определение логарифма; изображен график логарифмической функции, ее свойства; свойства логарифмов; алгоритм решения логарифмических неравенств, пример решения логарифмического неравенства, сводящегося к квадратному.
3. Изучение нового материала.
Решение логарифмических неравенств основано на монотонности логарифмической функции.
Алгоритм решения логарифмических неравенств:
А) Найти область определения неравенства (подлогарифмическое выражение больше нуля).
Б) Представить (если возможно) левую и правую части неравенства в виде логарифмов по одному и тому же основанию.
В) Определить, возрастающей или убывающей является логарифмическая функция: если t>1, то возрастающая; если 0 1, то убывающая.
Г) Перейти к более простому неравенству (подлогарифмических выражений), учитывая, что знак неравенства сохранится, если функция возрастает, и изменится, если она убывает.
Учебный элемент № 1.
Цель: закрепить решение простейших логарифмических неравенств
Форма организации познавательной деятельности учащихся: индивидуальная работа.
Задания для самостоятельной работы на 10 минут. Для каждого неравенства имеются несколько вариантов ответов, нужно выбрать верный и проверить по ключу.

КЛЮЧ: 13321, максимальное кол-во баллов – 6 б.
Учебный элемент № 2.
Цель: закрепить решение логарифмических неравенств, применяя свойства логарифмов.
Указания учителя. Вспомните основные свойства логарифмов. Для этого прочитайте текст учебника на с.92, 103–104.
Задания для самостоятельной работы на 10 минут.

КЛЮЧ: 2113, максимальное кол-во баллов – 8 б.
Учебный элемент № 3.
Цель: изучить решение логарифмических неравенств методом сведения к квадратному.
Указания учителя: метод сведения неравенства к квадратному состоит в том, что нужно преобразовать неравенство к такому виду, чтобы некоторую логарифмическую функцию обозначить новой переменной, получив при этом квадратное неравенство относительно этой переменной.

Применим метод интервалов.

Вы прошли первый уровень усвоения материала. Теперь вам придется самостоятельно выбрать метод решения логарифмических уравнений, используя все свои знания и возможности.
Учебный элемент № 4.
Цель: закрепить решение логарифмических неравенств, выбрав самостоятельно рациональный способ решения.
Задания для самостоятельной работы на 10 минут

Учебный элемент № 5.
Указания учителя. Молодцы! Вы освоили решение уравнений второго уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных и нестандартных ситуациях.
Задания для самостоятельного решения:

Указания учителя. Замечательно, если вы справились со всем заданием. Молодцы!
Оценка за весь урок зависит от числа набранных баллов по всем учебным элементам:
- если N ≥ 20, то вы получаете оценку “5”,
- при 16 ≤ N ≤ 19 – оценка “4”,
- при 8 ≤ N ≤ 15 – оценка “3”,
- при N 0; g (x ) > 0; k (x ) > 0; k (x ) ≠ 1.
Эти четыре неравенства составляют систему и должны выполняться одновременно. Когда область допустимых значений найдена, остается пересечь ее с решением рационального неравенства — и ответ готов.
Задача. Решите неравенство:
Для начала выпишем ОДЗ логарифма:
Первые два неравенства выполняются автоматически, а последнее придется расписать. Поскольку квадрат числа равен нулю тогда и только тогда, когда само число равно нулю, имеем:
x 2 + 1 ≠ 1;
x 2 ≠ 0;
x ≠ 0.
Получается, что ОДЗ логарифма — все числа, кроме нуля: x ∈ (−∞ 0)∪(0; +∞). Теперь решаем основное неравенство:

Выполняем переход от логарифмического неравенства к рациональному. В исходном неравенстве стоит знак «меньше», значит полученное неравенство тоже должно быть со знаком «меньше». Имеем:
(10 − (x 2 + 1)) · (x 2 + 1 − 1)
Задача. Решите неравенство:
Найдем область определения (ОДЗ) первого логарифма:
Решаем методом интервалов. Находим нули числителя:
Затем — нули знаменателя:
Отмечаем нули и знаки на координатной стреле:

Получаем x ∈ (−∞ 2/3)∪(1; +∞). У второго логарифма ОДЗ будет таким же. Не верите — можете проверить. Теперь преобразуем второй логарифм так, чтобы в основании стояла двойка:
Как видите, тройки в основании и перед логарифмом сократились. Получили два логарифма с одинаковым основанием. Складываем их:

Неравенство называется логарифмическим, если в нём содержится логарифмическая функция.
Методы решения логарифмических неравенств не отличаются от , за исключением двух вещей.
Во-первых, при переходе от логарифмического неравенства к неравенству подлогарифмических функций следует следить за знаком получающегося неравенства . Он подчиняется следующему правилу.
Если основание логарифмической функции больше $1$, то при переходе от логарифмического неравенства к неравенству подлогарифмических функций знак неравенства сохраняется, а если же меньше $1$, то меняется на противоположный.
Во-вторых, решение любого неравенства – промежуток, а, значит, в конце решения неравенства подлогарифмических функций необходимо составить систему из двух неравенств: первым неравенством этой системы будет неравенство подлогарифмических функций, а вторым – промежуток области определения логарифмических функций, входящих в логарифмическое неравенство.
Практика.
Основание логарифма равно $2>1$, поэтому знак не меняется. Пользуясь определением логарифма, получим:


